Энергетические характеристики электромагнитных волн. Вектор Умова–Пойнтинга

Энергия, переносимая электромагнитной волной, складывается из энергии электрического и магнитного полей, для которых объемная плотность энергии соответственно равна 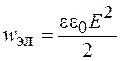и . Из (39.8) легко видеть, что объемные плотности электрического и магнитного полей в электромагнитной волне равны друг другу в любой момент времени, поэтому для объемной плотности энергии электромагнитной волны можно записать

. (41.1)

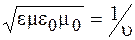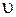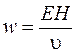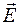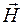Поскольку , где – скорость распространения волны, то из (41.1) следует, что или . Так как векторы и перпендикулярны друг другу и оба перпендикулярны вектору скорости 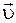, то последнее равенство можно представить в векторной форме:

. (41.2)

Вектор , равный векторному произведению векторов 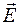и 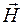, называется вектором Умова–Пойнтинга. Этот вектор направлен в сторону распространения волны, а его модуль равен мгновенному значению количества энергии, переносимой в единицу времени через единичную площадку, перпендикулярную направлению распространения электромагнитной волны. Единицей измерения вектора Умова–Пойнтинга является .

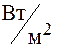Среднее значение энергии, переносимой в единицу времени через единичную площадку, перпендикулярную направлению распространения электромагнитной волны, называется интенсивностью волны и обозначается буквой 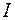. Как видно из приведенного определения, интенсивность есть скалярная величина, равная среднему значению модуля вектора Умова–Пойнтинга. Интенсивность также измеряется в :

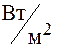, (41.3)

где угловые скобки означают среднее по времени значение.

Электромагнитная волна кроме энергии переносит также импульс, причем в вакууме импульс единицы объема связан с вектором Умова–Пойнтинга соотношением

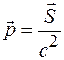, (41.4)

где 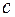– скорость света.

Так как электромагнитная волна переносит импульс, то при отражении или поглощении она оказывает давление. Давление равно среднему импульсу, передаваемому в единицу времени единице поверхности, перпендикулярной направлению распространения волны. Если импульс единицы объема равен 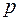, то при поглощении некоторым телом электромагнитной волны за время 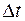ему будет передан импульс, сосредоточенный в объеме цилиндра 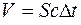, где 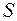– площадь поглощающей поверхности, перпендикулярной направлению распространения волны. Тогда по второму закону Ньютона сила давления 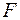будет равна 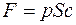, а давление 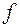составит

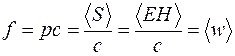, (41.5)

где, как и ранее, угловые скобки означают усреднение по времени. Если волна полностью отражается от поверхности тела, то передаваемый телу импульс окажется в два раза больше, чем при полном поглощении. В общем случае, если поверхность тела имеет коэффициент отражения 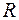, то давление, оказываемое электромагнитной волной при нормальном падении, будет равно с учетом (41.2)

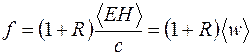, (41.6)

где 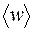– среднее значение объемной плотности энергии.