Излучение диполя

Одним из простейших излучателей электромагнитных волн является диполь. Предположим, что заряды, образующие диполь, совершают гармонические колебания в противофазе, в результате чего дипольный момент изменяется по закону

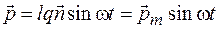, (42.1)

где 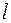– плечо диполя; 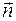– единичный вектор, направленный вдоль оси диполя от отрицательного заряда к положительному. Колеблющиеся заряды диполя создают в окружающем пространстве переменные электрическое и магнитное поля, т. е. диполь становится источником электромагнитных волн. Решение уравнений Максвелла показывает, что частота волны равна частоте 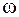колебаний зарядов диполя.

На расстояниях много меньших длины волны, излучаемой диполем (в ближней зоне), поле квазистационарное и токи смещения и переменное магнитное поле в этой области практически не играют заметной роли.

На расстояниях много больших длины волны ( 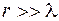) в так называемой волновой зоне излучение диполя представляет собой сферическую волну. Из уравнений Максвелла следует, что напряженности электрического и магнитного полей в момент времени 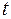определяются вторыми производными от дипольного момента в предшествующий момент времени :

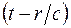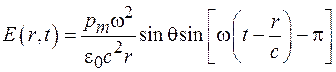, (42.2)

где 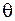– угол между осью диполя и направлением на точку наблюдения. Из выражения (42.2) видно, что амплитуда электромагнитной волны, излучаемой диполем, убывает с расстоянием гораздо медленнее, чем электростатическое поле диполя, которое изменяется пропорционально .

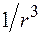Если представить, что диполь расположен в центре воображаемой сферы радиусом 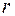(рис. 42.1), а его ось расположена вдоль линии, соединяющей полюса этой сферы, то вектор 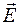лежит в плоскости, образованной осью диполя и направлением на точку наблюдения (меридиональная плоскость), и направлен по касательной к поверхности сферы. 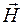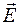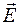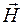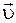При этом вектор направлен по касательной к широте, проведенной на поверхности сферы через точку наблюдения, и перпендикулярен одновременно вектору и направлению распространения волны так, что векторы , и образуют правую тройку векторов.

При перемещении точки наблюдения по меридиану на поверхности сферы амплитуда волны изменяется пропорционально 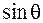. Она имеет максимальное значение на экваторе 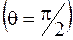и равна нулю на полюсах. Таким образом, излучение диполя максимально в направлениях, перпендикулярных его оси. Вдоль оси диполь не излучает.

Интенсивность волны 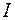пропорциональна квадрату амплитуды, поэтому из (42.2) следует, что

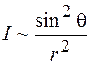. (42.3)

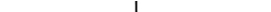Интенсивность излучения диполя так же, как и амплитуда, максимальна в направлениях, перпендикулярных оси диполя, и равна нулю вдоль оси. Зависимость интенсивности излучения от направления распространения волны в пространстве называется диаграммой направленности излучателя (антенны). Часто эту зависимость изображают в относительных единицах, нормируя интенсивность излучения на ее максимальное значение. Из (42.2), (42.3) следует, что для диполя диаграмма направленности описывается функцией 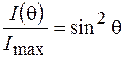, а ее вид изображен на рисунке 42.2.

Мощность излучения диполя 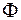можно найти, интегрируя интенсивность излучения по поверхности сферы. Вычисление интеграла дает следующее выражение:

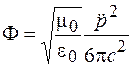, (42.4)

где 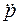– вторая производная дипольного момента по времени. Дифференцируя (42.1) и подставляя результат в последнее выражение, получим

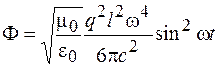, (42.5)

т. е. мощность излучения пропорциональна четвертой степени частоты. Если принять, что один из зарядов диполя неподвижный, а второй совершает гармонические колебания с частотой 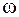так, что дипольный момент изменяется в соответствии с (42.1), то ускорение подвижного заряда будет равно 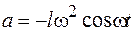и тогда соотношение (42.5) можно записать в виде

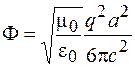. (42.6)

В таком виде формула оказывается верной не только для диполя, но и для любого заряда 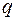, движущегося с ускорением 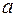. Это означает, что заряд, движущийся с ускорением, излучает электромагнитную волну, причем мощность излучения определяется выражением (42.6).

Вопросы для самоконтроля

1. Запишите волновое уравнение для электромагнитной волны в непроводящей среде: а) в декартовой системе координат; б) в одномерном случае; в) в операторной форме.

2. Перечислите основные свойства электромагнитных волн.

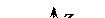3. Укажите направление распространения электромагнитной волны, для которой векторы 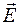и 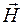направлены, как показано на рисунке.

4. Плоская электромагнитная волна падает по нормали на плоскопараллельную пластину из диэлектрика, расположенную в вакууме. Нарисуйте графики изменения напряженностей электрического 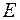и магнитного 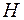полей падающей, отраженной и проходящей волн в фиксированный момент времени. Учесть отражение от обеих поверхностей пластины.

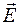5. В точке М на поверхности воображаемой сферы, в центре которой находится колеблющийся диполь, векторы и 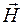в некоторый момент времени имеют направления, показанные на рисунке. Как направлена ось диполя? В какой из показанных точек А, В, С интенсивность излучения диполя: а) максимальная, б) минимальная?

6. От чего и как зависит интенсивность излучения диполя в произвольной точке дальней зоны?

7. От чего зависит доплеровское смещение частоты электромагнитных волн? Приведите примеры, где оно наблюдается.

Глава 5. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН