Интерференция плоских волн

Пусть в точку наблюдения А приходят две плоские монохроматические линейно-поляризованные волны (рис. 44.1), имеющие одинаковые частоту и направление колебаний векторов напряженности электрического поля:

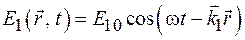, (44.1)

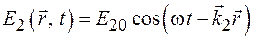. (44.2)

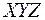Выберем систему координат таким образом, чтобы ось 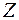совпала с линией пересечения волновых поверхносте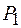й и 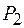, соответствующих одинаковой фазе колебаний. Интенсивность результирующей волны в точке А равна

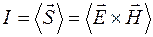, (44.3)

где – вектор Пойнтинга, а угловые скобки означают усреднение за период колебаний. Учитывая, что в электромагнитной волне 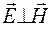, а напряженности электрического и магнитного полей связаны соотношением (40.7), получим

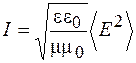. (44.4)

В соответствии с принципом суперпозиции 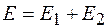и тогда

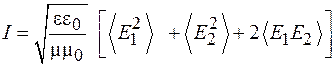. (44.5)

Усредняя за период колебаний квадраты напряженностей поле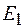й и 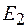, а также их произведение, получим

,

.

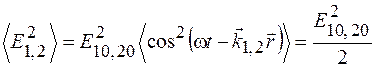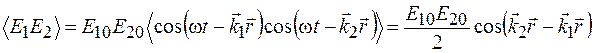Подставляя полученные выражения в формулу (44.5), запишем интенсивность результирующего колебания в виде

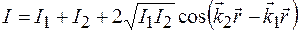, (44.6)

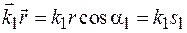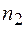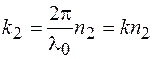где – интенсивности складываемых волн в точке наблюдения. Из рисунка 44.1 видно, что и . Если первая волна идет в точку наблюдения А в среде с показателем преломления , а вторая – в среде с показателем преломления , то и , где 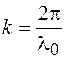– волновое число в вакууме. Тогда выражение (44.6) примет вид

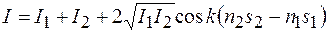. (44.7)

Произведение расстояния, пройденного волной в некоторой среде, на показатель преломления этой среды называется оптической длиной пути. Если в точку наблюдения приходят две волны, то разность оптических длин пути этих волн называется оптической разностью хода. Обозначив оптическую разность хода как 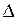, можно записать

, (44.8)

тогда выражение (44.7) примет вид

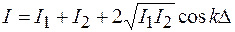. (44.9)

Полученное выражение показывает, что при наложении в точке наблюдения двух когерентных волн интенсивность в общем случае не равна сумме интенсивностей складываемых волн, а зависит от оптической разности хода этих волн до точки наблюдения. Явление наложения двух (или большего числа) когерентных волн, в результате которого происходит перераспределение интенсивности излучения в пространстве, называется интерференцией. 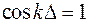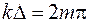Максимальная интенсивность будет, когда или , где 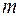– целое число. Так как 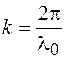, то условие максимума интенсивности можно выразить в виде

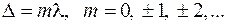, (44.10)

т. е. максимум интенсивности наблюдается в точках, для которых оптическая разность хода равна целому числу длин волн. Из (44.9) следует, что максимальная интенсивность

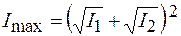. (44.11)

При выполнении условия максимумов колебания в точке наблюдения складываются в фазе (разность фаз 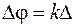составляет целое число ) и амплитуда результирующих колебаний равна сумме амплитуд приходящих в данную точку волн.

Если в точке наблюдения 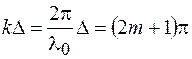, т. е. оптическая разность хода равна нечетному числу полуволн:

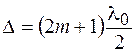, где 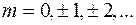, (44.12)

то интенсивность излучения имеет минимальное значение (условие минимума интенсивности):

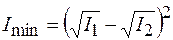. (44.13)

В этом случае колебания в точке наблюдения складываются в противофазе (разность фаз 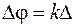составляет нечетное число 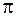) и амплитуда результирующих колебаний равна разности амплитуд приходящих в данную точку волн.

Если на пути интерферирующих плоских волн поставить экран Э (рис. 44.1), то на экране возникнет интерференционная картина, имеющая форму чередующихся темных и светлых полос, параллельных линии пересечения волновых поверхностей интерферирующих плоских волн.

Условия максимумов и минимумов получены на примере интерференции плоских волн, однако то же самое будет иметь место при интерференции волн с произвольными волновыми поверхностями.