Интерференция волн от двух когерентных источников

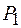Пусть имеются два точечных когерентных источника и 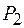, расположенные на расстоянии 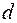друг от друга в плоскости П (рис. 46.1). Интерференционная картина наблюдается на экране Э, установленном на расстоянии 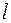. Поместим начало отсчета координаты 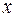в точку О, лежащую на перпендикуляре к плоскости экрана, проходящем через середину отрезка 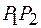. Возьмем точку А с координатой 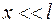и найдем оптическую разность хода 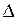лучей от источников 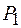и 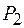до этой точки. Опустив перпендикуляр из точки 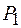на прямую 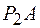, из 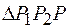получим

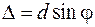. (46.1)

Поскольку 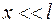, то угол 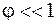и для 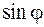можно приближенно записать . Тогда выражение (46.1) примет вид

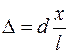. (46.2)

Подставив в левую часть полученного соотношения условия максимумов (44.10) и минимумов (44.12), найдем координаты светлых 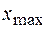и темных 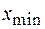полос:

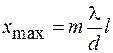, (46.3)

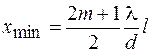, (46.4)

где

Интерференционная картина имеет вид чередующихся темных и светлых полос, перпендикулярных линии, соединяющей точечные источники. В центре интерференционной картины (точка О) всегда наблюдается светлая полоса. Ширина полос 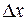равна расстоянию между двумя соседними максимумами (или минимумами):

. (46.5)

Из последнего равенства следует, что ширина интерференционных полос зависит от соотношения длины волны и расстояния между источниками, а также расстояния до экрана.

Интерференцию волн от двух когерентных источников впервые наблюдал Т. Юнг в 1802 г. В опыте Юнга интерференционная картина наблюдалась в солнечном свете, который, как известно, не является когерентным. Для получения когерентного излучения Юнг поставил на пути солнечного света ширму с маленьким отверстием. Это отверстие вырезало из падающего солнечного света малую область, в пределах которой излучение имеет достаточно высокую когерентность. Далее это излучение освещало вторую ширму, в которой булавкой были проделаны два близко расположенных отверстия 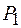и 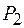, которые можно рассматривать как два точечных источника когерентных волн. Свет, прошедший через эти отверстия, давал на экране интерференционную картину.