Стоячие электромагнитные волны
Стоячие волны возникают в результате интерференции двух монохроматических плоских волн с одинаковой частотой, распространяющихся в противоположных направлениях.
Пусть плоская монохроматическая волна отражается от поверхности, расположенной перпендикулярно направлению распространения волны. После отражения волновой вектор поменяет направление на противоположное и при этом вектор 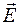 приобретет дополнительный сдвиг фазы
приобретет дополнительный сдвиг фазы 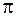 (так как отражение происходит от оптически более плотной среды). Тогда для падающей и отраженной волн можно записать
(так как отражение происходит от оптически более плотной среды). Тогда для падающей и отраженной волн можно записать
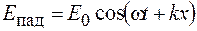 ,
,  ,
,
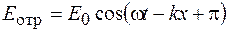 ,
,  .
.
Эти волны будут интерферировать, и по принципу суперпозиции для результирующей стоячей волны получим следующие уравнения:
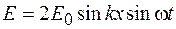 , (49.1)
, (49.1)
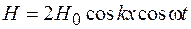 . (49.2)
. (49.2)
 Из формул (49.1) и (49.2) следует первое важное отличие стоячей волны от бегущей: в стоячей волне колебания векторов
Из формул (49.1) и (49.2) следует первое важное отличие стоячей волны от бегущей: в стоячей волне колебания векторов 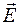 и
и 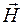 сдвинуты по фазе на
сдвинуты по фазе на 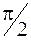 , т. е. в те моменты, когда напряженность электрического поля максимальна, напряженность магнитного поля равна нулю и наоборот (рис. 49.1). В бегущей волне колебания
, т. е. в те моменты, когда напряженность электрического поля максимальна, напряженность магнитного поля равна нулю и наоборот (рис. 49.1). В бегущей волне колебания 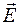 и
и 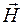 происходят в фазе.
происходят в фазе.
Как видно из выражений (49.1) и (49.2), амплитуда колебаний векторов 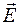 и
и 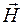 в стоячей волне в разных точках пространства оказывается различной. Точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны. Точки, в которых амплитуда имеет максимальное значение, называются пучностями. Для электрического поля амплитуда равна нулю, если
в стоячей волне в разных точках пространства оказывается различной. Точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны. Точки, в которых амплитуда имеет максимальное значение, называются пучностями. Для электрического поля амплитуда равна нулю, если 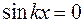 . Отсюда следует, что узлы находятся в точках с координатами
. Отсюда следует, что узлы находятся в точках с координатами
 (49.3)
(49.3)
Пучности электрического поля расположены в точках, где 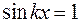 , т. е.
, т. е.
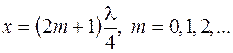 (49.4)
(49.4)
Из этих выражений видно, что расстояние между смежными узлами (или пучностями) равно половине длины бегущей волны. Таким же образом легко убедиться, что узлы магнитного поля находятся в точках с координатами, определяемыми выражением (49.4), а пучности – выражением (49.3), т. е. в стоячей волне узлы электрического поля совпадают с пучностями магнитного поля и наоборот. При этом на отражающей поверхности находятся узел электрического поля и пучность магнитного. Если отражение происходит от оптически менее плотной среды, то сдвиг фазы на 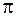 получит вектор
получит вектор 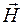 и на отражающей поверхности будут пучность электрического поля и узел магнитного.
и на отражающей поверхности будут пучность электрического поля и узел магнитного.
Из выражений (49.1) и (49.2) следует, что колебания во всех точках, расположенных между двумя соседними узлами, происходят в одной фазе. При переходе через узел фаза колебаний изменяется на 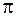 . При этом фазовая поверхность не перемещается в пространстве, чем и объясняется само название стоячей волны.
. При этом фазовая поверхность не перемещается в пространстве, чем и объясняется само название стоячей волны.
Объемные плотности энергии электрического и магнитного полей 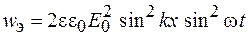 и
и  соответственно. Изменения энергии электрического и магнитного полей в стоячей волне происходят с удвоенной частотой и в противофазе. Это означает, что в стоячей волне происходит периодическое преобразование энергии электрического и магнитного полей так, что в моменты, когда энергия электрического поля максимальна, энергия магнитного поля равна нулю и наоборот. В этом тоже заключается существенное отличие стоячих волн от бегущих. Используя формулу (39.10), легко убедиться, что максимальные значения объемной плотности энергий электрического и магнитного полей равны. Для стоячей волны модуль вектора Пойнтинга
соответственно. Изменения энергии электрического и магнитного полей в стоячей волне происходят с удвоенной частотой и в противофазе. Это означает, что в стоячей волне происходит периодическое преобразование энергии электрического и магнитного полей так, что в моменты, когда энергия электрического поля максимальна, энергия магнитного поля равна нулю и наоборот. В этом тоже заключается существенное отличие стоячих волн от бегущих. Используя формулу (39.10), легко убедиться, что максимальные значения объемной плотности энергий электрического и магнитного полей равны. Для стоячей волны модуль вектора Пойнтинга 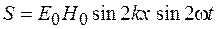 , а его среднее за период колебаний значение равно нулю. Это означает, что стоячая волна не переносит энергию в пространстве.
, а его среднее за период колебаний значение равно нулю. Это означает, что стоячая волна не переносит энергию в пространстве.
Стоячие волны в видимом диапазоне длин волн впервые зарегистрировал Винер в 1890 г. Он установил перед зеркалом под небольшим углом  прозрачную пластинку с нанесенным на нее фоточувствительным слоем (рис. 49.2) и после проявления обнаружил на ней чередующиеся темные и светлые полосы, центры которых соответствовали положению узлов и пучностей электрического поля. Опыт Винера явился одним из прямых доказательств электромагнитной природы света.
прозрачную пластинку с нанесенным на нее фоточувствительным слоем (рис. 49.2) и после проявления обнаружил на ней чередующиеся темные и светлые полосы, центры которых соответствовали положению узлов и пучностей электрического поля. Опыт Винера явился одним из прямых доказательств электромагнитной природы света.
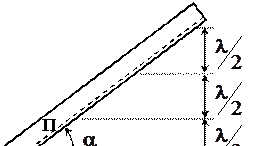 Упругие волны также могут образовывать стоячую волну. Наглядным примером стоячей упругой волны являются колебания струны с закрепленными краями. Их можно наблюдать на любом струнном музыкальном инструменте (гитара, арфа и др.).
Упругие волны также могут образовывать стоячую волну. Наглядным примером стоячей упругой волны являются колебания струны с закрепленными краями. Их можно наблюдать на любом струнном музыкальном инструменте (гитара, арфа и др.).
Дата добавления: 2015-08-08; просмотров: 2013;
