Интерферометр Фабри–Перо

В рассмотренном примере с плоскопараллельной пластинкой учитывалась интерференция двух волн, отраженных от передней и задней поверхностей пластинки. В действительности падающее излучение будет многократно отражаться от поверхностей пластинки, и волны, испытавшие два и более отражения, внесут свой вклад в результат интерференции. Если коэффициент отражения 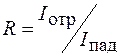от поверхности пластинки мал, то интенсивность света после каждого отражения будет быстро уменьшаться и влиянием лучей, испытавших многократные отражения, можно пренебречь. Если же коэффициент отражения достаточно велик ( 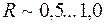), то необходимо рассматривать многолучевую интерференцию.

Рассмотрим систему, состоящую из двух параллельных плоских пластин, разделенных воздушным промежутком толщиной 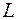(рис. 48.1). Пусть на внутренние поверхности этих пластин нанесено отражающее покрытие с коэффициентом отражения 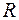. Такая система называется интерферометром Фабри–Перо. Если на интерферометр Фабри–Перо направить плоскую монохроматическую волну интенсивностью 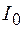, то часть света отразится, а остальная часть пройдет через интерферометр. Интенсивность прошедшего света 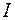будет определяться интерференцией всех волн, испытавших многократные отражения на поверхностях интерферометра (волны 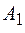, , 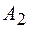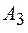и т. д. на рисунке 48.1).

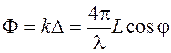Каждая последующая волна, начиная со второй, будет приобретать дополнительный сдвиг фазы , где 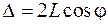. Это следует из выражения (47.3), которое при 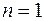с учетом двойного отражения дает для разности хода 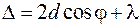. Дополнительную разность хода 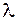, возникающую при отражении, можно опустить, поскольку она не влияет на результат интерференции.

Можно показать, что в результате интерференции всех волн интенсивность прошедшего света определяется следующим выражением:

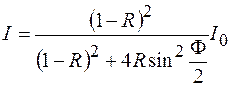. (48.1)

Интенсивность отраженного света 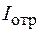можно определить по закону сохранения энергии из условия 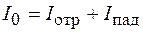. С учетом (48.1) получим

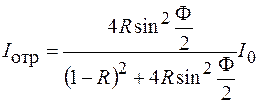. (48.2)

Из выражения (48.1) видно, что интенсивность проходящего через интерферометр света будет максимальна при условии 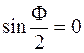. Если угол падения 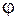равен 0, т. е. зеркала перпендикулярны падающему лучу, это будет иметь место в случае, ес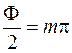ли или 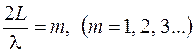. Отсюда получаем, что коэффициент пропускания будет максимален для длин волн 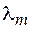, удовлетворяющих соотношению

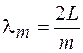. (48.3)

Равенство (48.3) означает, что максимальное пропускание интерферометра будет иметь место для излучения, у которого на длине интерферометра укладывается целое число полуволн. При этом условии все отраженные от зеркал волны складываются в одной фазе.

Если 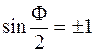, т. е.

, (48.4)

то пропускание интерферометра будет минимальным. Это будет иметь место в случае, если на двойной длине интерферометра укладывается нечетное число полуволн.

На рисунке 48.2 приведены графики зависимости коэффициента пропускания интерферометра 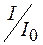от длины волны 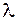для различных коэффициентов отражения 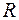. Из рисунка видно, в результате многолучевой интерференции интерферометр Фабри–Перо приобретает резонансные свойства. Из сравнения графиков видно, что чем больше коэффициент отражения зеркал, тем резче резонансные пики. Так как 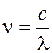, то из (48.3) для резонансных частот получается следующее выражение:

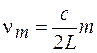. (48.5)

Резонансные частоты расположены эквидистантно с интервалом

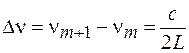. (48.6)

Можно показать, что добротность интерферометра Фабри–Перо определяется выражением

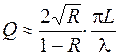. (48.7)

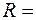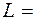Полагая 0,9; 1 см; 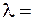0,5 мкм, получим 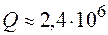. Приведенная оценка показывает, что интерферометр Фабри–Перо в оптическом диапазоне длин волн представляет собой высокодобротную резонансную систему, поэтому он широко используется для точных спектральных измерений, когда другие методы не обеспечивают требуемую точность. Изменяя угол падения 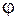излучения, можно перестраивать резонансные частоты, для которых коэффициент пропускания будет максимален.