Интерферометры

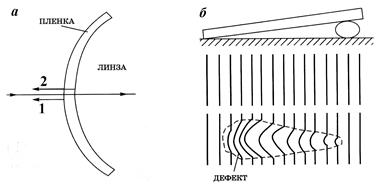
Просветление оптики.На границе раздела воздух – стекло отражается 4% энергии световой волны. Поэтому при наличии в оптическом приборе достаточного количества линз, зеркал, преломляющих тел до наблюдателя доходит малая часть первоначальной энергии световой волны.

Чтобы увеличить освещенность изображения с помощью интерференции убирают отраженные лучи. Для этого на поверхность линзы наносят тонкую пленку, у которой показатель преломления меньше, чем показатель преломления линзы. В этом случае, наряду с лучом 1, отраженным от поверхности линзы, возникает луч 2, отраженный от поверхности пленки (рис. 4.8а). Эти лучи должны быть когерентными, что бы отражаясь, они гасили дуг друга. Толщина пленки определяется из условия

.

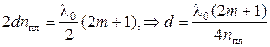В этом случае происходит перераспределение световой энергии; она вся проходит в линзу, отраженной волны не будет.

Определение качества обработки поверхностей.На исследуемую поверхность кладут плоскопараллельную пластинку так, чтобы создать воздушный зазор между исследуемой поверхностью и пластинкой (рис. 4.8б). По искажению картины интерференции можно обнаружить дефекты ее обработки (царапины, шероховатость), так как в места нахождения дефекта искажена правильная картина чередования светлых и темных полос.

Интерферометры.Это приборы, в которых наблюдаемая картина интерференции служит для практических целей (для точных измерений длин волн, размеров малых предметов, показателей преломления газов, определения шероховатости поверхностей деталей и др.).

Картина интерференции получается пространственным делением пучка света на два или большее количество когерентных пучка, создания между ними оптической разности хода и затем наложения с целью получения картины интерференции.

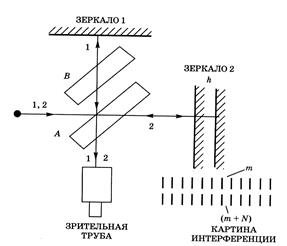
Существуют различные виды таких приборов; здесь рассматривается двух лучевой интерферометр Майкельсона (рис. 4.9).

пластины В и А и попадает в зрительную трубу. Пластинка В необходима для того, чтобы создать одинаковые условия для лучей 1 и 2. Если зеркала 1 и 2 будут взаимно перпендикулярны, то на экране в зрительной трубе будет наблюдаться светлое или темное пятно. Для создания картины интерференции одно из зеркал немного наклоняют, это приводит к изменению оптической разности хода лучей, и на экране будут наблюдаться полосы равной толщины.

Если, например, вместо зеркала 1 поместить деталь, шероховатость которой надо определить, то по искажению линий интерференции можно определить степень шероховатости.

Если надо определить размер h малого предмета, то совместив один из концов этого предмета с зеркалом 2, перемещают это зеркало до другого конца предмета, считая число полос прошедших мимо указателя зрительной трубы. Тогда

,

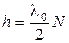где N – число темных полос, прошедших мимо указателя.

Лекция 5

5.1. Дифракция света. Принцип Гюйгенса – Френеля. Метод зон Френеля

Под дифракцией света понимают явление непрямолинейного распространения света, проникновение его в область геометрической тени, огибание им препятствий. Основные закономерности явления дифракции можно понять на основе принципа Гюйгенса – Френеля.

Согласно принципу Гюйгенса – Френеля каждая точка фронта волны является источником вторичных когерентных волн. Этот принцип сводит явление дифракции к интерференции вторичных когерентных волн. Между явлениями интерференции и дифракции нет принципиального различия: если рассматривать наложение малого числа когерентных волн – это будет интерференция, если большого – дифракция.

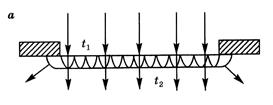
Покажем, как можно объяснить явление дифракции с помощью принципа Гюйгенса – Френеля. Пусть на преграду, в которой имеется щель, падает плоская волна. На рис. 5.1 она изображена в тот момент времени t₁, когда фронт волны занимает положение в этой щели. Найдем положение фронта волны в следующий момент времени t₂ = (t₁ + ∆t). Он отстоит от первоначального положения на достаточно малый интервал времени, за который вторичные волны проходят расстояние R, значительно меньшее размеров щели d (R = c∆t << d).

Каждая точка фронта волны в соответствии с принципом Гюйгенса – Френеля является источником вторичных волн, которые за время ∆t проходят расстояние R, и фронт вторичной волы будет представлять собой сферу. Положение фронта волны в момент t₂ можно найти как огибающую фронтов вторичных волн (рис.5.1). Учитывая, что скорость волны в каждой точке фронта волны перпендикулярна к ней, можно видеть, что имеются участки фронта волны, которые обеспечивают проникновение света в область геометрической тени. Если размеры этих участков фронта волны будут соизмеримы с размерами щели, то тогда явление дифракции света будет наблюдаться; если же они будут существенно меньше размеров щели, то явление дифракции, хоть и будет существовать, но будет незаметным.

На рис. 5.2 показано в определенный момент времени положение фронта волны, излучаемой точечным источником S монохроматического излучения (λ₀). Найдем результирующую амплитуду волн, приходящих от всех точек фронта волны в точку наблюдения Р. В этой точке будет иметь место результат сложения вторичных когерентных волн, испускаемых каждым малым участком фронта волны.

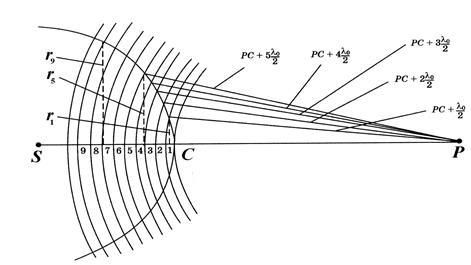
Для расчета результирующей амплитуды используем метод разбиения фронта волны на зоны, предложенный Френелем. Для этого из точки наблюдения проводят сферы радиусов 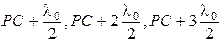и т.д. Эти сферы разбивают фронт волны на зоны Френеля. При этом зоны Френеля обладают следующими свойствами.

1. Волны, приходящие в точку наблюдения от соседних зон Френеля имеют оптическую разность хода равную λ₀/2 или разность фаз, равную π.

2. При не слишком больших значениях номера mзоны площади зон примерно одинаковы.

3. Для амплитуды волн, приходящих от разных зон Френеля, в точку наблюдения, справедливы следующие соотношения:

А₁ > А₂ > А₃ > А₄ > А₅ …, .

Cувеличением номера зоны будет уменьшаться амплитуда волны, приходящей в точку наблюдения, от рассматриваемой зоны.

Введение зон Френеля позволяет найти результирующую амплитуду в точке наблюдения через амплитуду волн от всех зон Френеля.

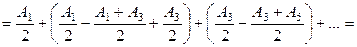
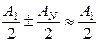.(5.1)

В формуле (5.1) учтено, что при значении N, стремящемуся к бесконечности, вкладом зоны Френеля с номером Nможно пренебречь, по сравнению с вкладом от первой зоны Френеля.

Итак, в точке наблюдения результирующая амплитуда всех вторичных волн, испущенных от всех точек фронта волны, равна половине амплитуды вторичной волны, приходящей в точку наблюдения от первой зоны.

Метод зон Френеля позволяет предложить способы для получения значений амплитуды в точнее наблюдения, превышающих значение А₁/2. Так, если закрыть непрозрачным экраном все зоны Френеля, кроме первой, то тогда можно увеличить амплитуду результирующей волны в два раза (А_Р = А₁), а интенсивность – в четыре раза.

Для дальнейшего увеличения А_Р можно на пути волны поставить зонную пластинку, которая закрывает все четные зоны Френеля, что приводит к следующему результату:

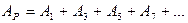
Максимальное увеличение амплитуды А_Р можно получить с помощью фазовой зонной пластинки, которая изменяет фазу волн, идущих в точку наблюдения от четных зон Френеля на значение, равное π: