Пространственная и временная когерентности
 Определим, при каких же условиях полученные выше волны можно считать когерентными. Учтем, что любая волна представляет собой результат наложения большого количества колебаний с различными частотами, т. е. световая волна характеризуется спектром (рис. 4.3). Если этот спектр узок, то свет воспринимается как монохроматический с частотой ω0. Но и такую волну можно рассматривать как волну, полученную от наложения двух волн с близкими частотами: ω0 и ω0 + ∆ω, где ∆ω – ширина спектра, т. е. интервал между частотами, интенсивность которых I = I0/2.
Определим, при каких же условиях полученные выше волны можно считать когерентными. Учтем, что любая волна представляет собой результат наложения большого количества колебаний с различными частотами, т. е. световая волна характеризуется спектром (рис. 4.3). Если этот спектр узок, то свет воспринимается как монохроматический с частотой ω0. Но и такую волну можно рассматривать как волну, полученную от наложения двух волн с близкими частотами: ω0 и ω0 + ∆ω, где ∆ω – ширина спектра, т. е. интервал между частотами, интенсивность которых I = I0/2.
При наложении волн с близкими частотами в некоторой точке пространства возникают биения (рис. 4.4).
|
При ∆t << ТБ интенсивность результирующей волны I ≠ I1 + I2 ,
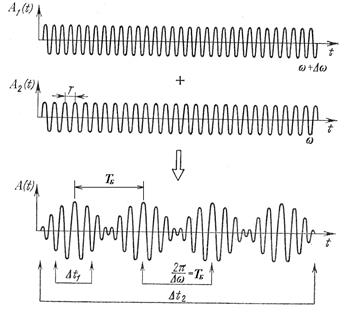 а при ∆t > ТБ I = I1 + I2. В первом случае мы должны сделать вывод, что накладывающиеся волны когерентные между собой, а во втором – не когерентные. Т. е. об одном и том же процессе получили два противоположных вывода. В связи с этим и вводится понятие ∆t = τ (время когерентности) - это наибольший промежуток времени при усреднении по которому накладывающиеся волны еще остаются когерентными.
а при ∆t > ТБ I = I1 + I2. В первом случае мы должны сделать вывод, что накладывающиеся волны когерентные между собой, а во втором – не когерентные. Т. е. об одном и том же процессе получили два противоположных вывода. В связи с этим и вводится понятие ∆t = τ (время когерентности) - это наибольший промежуток времени при усреднении по которому накладывающиеся волны еще остаются когерентными.
За τ принимают период биений(τ = ТБ).
|
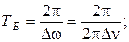 т.к.
т.к.
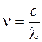

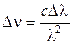 ,
, 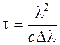 .
.
Т. о. время когерентности зависит от ширины спектра накладывающихся волн. Когерентность, зависящую от ширины спектра, принято называть временной когерентностью.Время когерентности позволяет определить длину когерентности
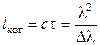 .(4.1)
.(4.1)
Длина когерентности определяет расстояние, при прохождении которого, накладывающиеся волны утрачивают свойство когерентности.
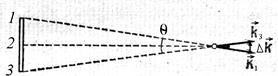 Кроме временной когерентности проявляется еще пространственная когерентность.Она обусловлена тем, что источники света характеризуются угловыми размерами. Пусть имеется источник света. Свет, приходящий от разных точек источника, в некоторую точку пространства А будет иметь разное направление вектора
Кроме временной когерентности проявляется еще пространственная когерентность.Она обусловлена тем, что источники света характеризуются угловыми размерами. Пусть имеется источник света. Свет, приходящий от разных точек источника, в некоторую точку пространства А будет иметь разное направление вектора 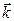 (волновое число) (рис. 4.5). Угловой размер удаленного источника Ө можно выразить так:
(волновое число) (рис. 4.5). Угловой размер удаленного источника Ө можно выразить так:
|
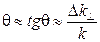 .
.
Величину rk 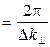 - называют радиусом когерентности. Он определяет максимальное расстояние в направлении перпендикулярном направлению света, на котором волны остаются еще когерентными между собой.
- называют радиусом когерентности. Он определяет максимальное расстояние в направлении перпендикулярном направлению света, на котором волны остаются еще когерентными между собой.
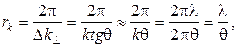 (4.2)
(4.2)
т. е. радиус когерентности зависит от углового размера источника и среднего значения длин волн, приходящих от этого источника. Определим длину и радиус когерентности лучей видимого диапазона, приходящих от Солнца. Учтем, что угловой размер Солнца Ө= 10-2 радиана, среднее значение длины волны лучей видимого диапазона λ~ 5 10-7 м, а ширина видимого диапазона ∆λ~ 2, 5۠·10-7м, тогда lког= 1 мкм, а rk= 50 мкм.
Дата добавления: 2015-08-08; просмотров: 880;
