Интерференция на тонкой пленке
Луч света длиной волны λ падает на пленку толщиной dпод углом падения i(рис. 4.6) и делится на два: луч 1 отражается от верхней грани, а луч 2 преломляется, проходит в пленка расстояние АВ, затем отражается от нижней грани, проходит расстояние ВС и затем преломляется. Два луча собираются линзой в одной точка, расположенной в фокальной плоскости линзы. Для расчета картины интерференции на экране найдем оптическую разность хода лучей 1 и 2.
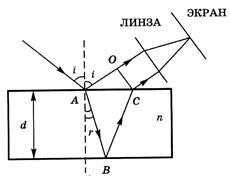Разность хода лучей 1 и 2 в точке Аравна нулю, так как они двигались вместе, составляя луч падающего на пластинку света. После линии ОС (она перпендикулярна лучам 1 и 2) их разность хода не изменяется, так как линза не дает дополнительной разности хода для этих лучей. Поэтому оптическая разность хода возникает при переходе лучей от точки А к линии ОС:
|
Оптическим ходом луча называют произведение
геометрического хода (АВ +ВС) на показатель
преломления среды, в которой распространяется луч. На участке АО луч 1 распространяется в воздухе, для которого nВ = 1. В формулу для оптической разности хода введено слагаемое λ0/2, так как вектор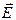 
напряженности луча 1 при отражении от оптически более плотной среды изменяет свою фазу на π или луч 1 теряет полволны. λ0 – длина волны в вакууме. Подставляя параметры пленки и угол падения в формулу (4.3), для оптической разности хода можно окончательно записать:
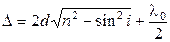.(4.4)
Для данного примера условия наблюдения максимумов и минимумов будут выглядеть таким образом:
максимумы: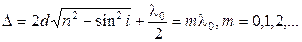 
минимумы: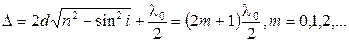 
Отметим, что для наблюдения интерференционной картины нужно брать тонкую пленку, чтобы для естественного света лучи 1 и 2 после линии ОСбыликогерентными: ОС ≤ rк (из за пространственной когерентности) и ∆ ≤ lк (из за временной когерентности).
Как видно из формулы (4.4), оптическую разность хода лучей ∆ можно изменять либо изменением угла падения i, либо изменяя толщину пленки d. Рассмотрим полученные интерференционные картины.
Если на пленку одинаковой толщины d падает монохроматический свет под одним и тем же углом i и выполняется условие максимума, то пленка в отраженных лучах будет светлой (имеющий цвет падающей длины волны). При выполнении условия минимума отраженных лучей не будет. Свет не отражаясь, проходит через пленку.
|
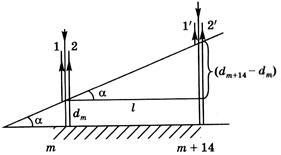Если на пленку с линейно изменяющейся толщиной d (клин) (рис. 4.7) падает монохроматический свет под одним и тем же углом i, то в отраженных лучах будут наблюдаться полосы равной толщины. Если на этот клин направить белый свет, то максимумы превратятся в спектры.
В пределах каждого максимума цвет будет плавно меняться от красного к фиолетовому.
Дата добавления: 2015-08-08; просмотров: 1159;