Дифракционная решетка. Рассмотрим плоскую периодическую структуру из параллельных щелей, разделенных непрозрачными промежутками
Рассмотрим плоскую периодическую структуру из параллельных щелей, разделенных непрозрачными промежутками. На практике обычно роль щелей выполняют прозрачные участки стеклянных пластинок, разделенных непрозрачными штрихами, наносимыми с помощью алмазных резцов. Такие структуры и называют дифракционными решетками. Современные технологии позволяют изготовлять решетки, лучшие из которых имеют свыше 1000 штрихов на длине в 1 мм при полном числе штрихов до 200000. Суммарная ширина щели а и непрозрачного промежутка bназывается периодом решетки d= (a+ b).
|
Пусть на решетку с Nщелями (рис. 5.5) падает плоская монохроматическая волна. За решеткой располагается линза, в фокальной плоскости которой находится экран. Каждая из щелей дает на экране картину, описываемую кривой, изображенной на рис. 5.4б. Картины от всех щелей придут на одно и то же место экрана. Если бы колебания, приходящие в точку М от разных щелей, были не когерентными, результирующая картина от Nщелей отличалась бы от картины, созданной одной щелью, лишь тем, что интенсивности во всех точках возросли бы в Nраз.
В дальнейшем мы будем полагать, что радиус когерентности падающей волны превышает длину решетки, поэтому колебания от всех щелей можно считать когерентными. Волны же идущие от двух соседних щелей будут отличаться по фазе колебаний на величину
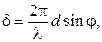
где λ – длина волны в данной среде, dsinφ– разность хода для лучей, идущих под углом φ, например, от крайних точек соседних щелей (рис. 5.5). При наложении когерентных волн происходит перераспределение световой энергии в фокальной плоскости линзы (рис. 5.5).
|
Основная часть световой энергии попадает в главные максимумы. Условие главных максимумов определяет выражение:
.
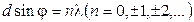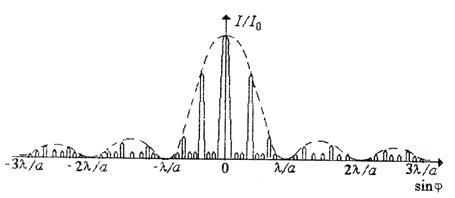
Интенсивность главных максимумов в N2раз больше чем интенсивность в этом направлении φ от одной щели. Между главными максимумами наблюдаются вторичные максимумы, разделенные добавочными минимумами. В дифракционной картине для направлений φ, удовлетворяющих условию asinφ= mλ0, наблюдаются главные минимумы.
На рис. 5.6 приведено распределение интенсивности света решеткой с N= 4 и d/a= 3. При весьма большом числе щелей картина на экране будет представлена узкими очень яркими полосками, разделенными почти темными промежутками, ибо вторичные максимумы очень слабы по сравнению с главными. Расстояние между главными максимумами возрастает с уменьшением периода решетки d= (a+ b).
Дата добавления: 2015-08-08; просмотров: 1027;