Интерференция сферических волн

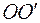Пусть на оси расположены два точечных источника 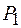и 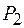, излучающие сферические волны одинаковой частоты (рис. 45.1). Интенсивность в произвольной точке А экрана, удаленной на расстояние 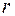от центра экрана 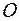, будет определяться оптической разностью хода 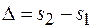лучей, приходящих в эту точку от источников (для простоты показатель преломления среды взят равным ). Для всех точек экрана, удаленных на одинаковое расстояние 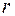от центра (т. е. для точек окружности с центром 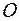) оптическая разность хода, а значит и интенсивность, будут одинаковы. Отсюда следует, что интерференционная картина, возникающая при наложении двух сферических волн, имеет вид чередующихся темных и светлых колец, центр которых лежит на прямой, соединяющей точечные источники.

Интенсивность в центре экрана ( 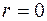) будет зависеть от расстояния 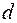между источниками. Если 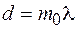, где 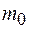– целое число, то в центре будет максимум интенсивности; если же 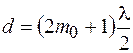, то в точке 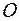будет наблюдаться минимум интенсивности.

Если один из источников (например, ) удален в бесконечность, то от него приходит плоская волна и на экране будет наблюдаться интерференция плоской и сферической волн. В этом случае картина также будет иметь форму колец и ее можно получить с помощью установки для наблюдения колец Ньютона, изображенной на рисунке 45.2. Плосковыпуклая линза Л положена сферической поверхностью на плоскопараллельную пластину П. Установка освещается сверху светом, а интерференционная картина наблюдается в отраженном свете. Падающий луч 1 проходит через плоскую поверхность линзы и частично отражается от сферической поверхности (луч 2). Оставшаяся часть света проходит через зазор 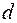между линзой и плоской пластиной и после частичного отражения от пластины также идет в обратном направлении по отношению к падающему лучу (луч 3). Между отраженными лучами 2 и 3 возникает оптическая разность хода D:

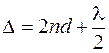, (45.1)

где n – показатель преломления среды, заполняющей зазор. Дополнительная разность хода 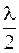возникает при отражении одного из интерферирующих лучей от оптически более плотной среды (обычно это имеет место для луча 3).

По теореме Пифагора 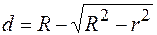, где r – расстояние от центра интерференционной картины до точки наблюдения. Диаметр линзы обычно значительно меньше радиуса кривизны ее поверхности, т. е. 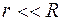и тогда можно приближенно записать . Подставив полученное выражение для 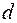в (45.1), запишем оптическую разность хода в виде

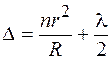. (45.2)

Радиусы темных и светлых колец определим из условия максимумов и минимумов интенсивности в интерференционной картине:

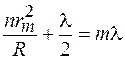– светлое кольцо, (45.3)

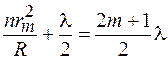– темное кольцо, (45.4)

где 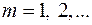– номер кольца.

Отсюда находим выражения для радиусов светлого и темного колец:

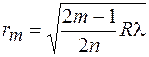– радиус светлого кольца, (45.5)

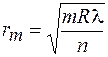– радиус темного кольца. (45.6)

В центре интерференционной картины в отраженном свете всегда наблюдается темное пятно, так как при 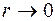оптическая разность хода 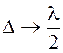, как это следует из (45.2).

Кольца Ньютона можно наблюдать и в проходящем свете. Из закона сохранения энергии следует, что интерференционные картины в проходящем и отраженном свете являются дополнительными, т. е. в том месте, где в отраженном свете наблюдается темное кольцо, в проходящем свете будет светлое кольцо и наоборот. Поэтому в проходящем свете радиусы светлых колец определяются выражением (45.6), а темных – выражением (45.5).