Уравнение непрерывности

Возьмем произвольную замкнутую поверхность 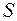, ограничивающую объем 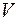. Величина заряда, находящегося внутри этой поверхности,

,

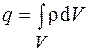где 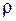– объемная плотность заряда.

Если через объем 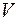протекают токи, то величина заряда изменяется во времени, причем скорость изменения заряда 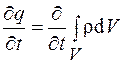. Поток вектора плотности тока 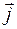через поверхность 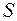равен величине заряда, вытекающего из объема 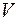в единицу времени. Поэтому можно записать

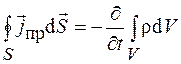. (37.1)

В соответствии с теоремой Остроградского–Гаусса правую часть уравнения (37.1) можно записать в виде 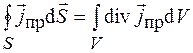, и тогда это уравнение примет следующий вид:

.

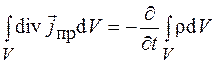Полученное уравнение должно выполняться для любого объема 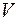в любой момент времени, а это может быть только в том случае, если

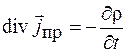. (37.2)

Уравнение (37.2) называется уравнением непрерывности и выражает закон сохранения заряда в дифференциальной форме.