Операторы Гамильтона и Лапласа
Под оператором понимается некоторое правило или последовательность действий, в результате применения которых к функции 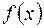 она преобразуется в новую функцию
она преобразуется в новую функцию  . Если обозначить оператор буквой L, то его действие на функцию
. Если обозначить оператор буквой L, то его действие на функцию 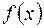 символически записывают следующим образом:
символически записывают следующим образом:
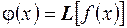 . (35.1)
. (35.1)
Примером оператора является так называемый "дифференциальный оператор" 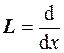 . Действие данного оператора на какую-либо функцию сводится к взятию производной этой функции, т. е.
. Действие данного оператора на какую-либо функцию сводится к взятию производной этой функции, т. е. 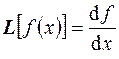 . Например, если
. Например, если 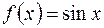 , то
, то 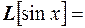
 .
.
В теории поля часто используется оператор Гамильтона, который принято обозначать как 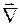 (читается – "набла"). Этот дифференциальный оператор имеет следующий вид:
(читается – "набла"). Этот дифференциальный оператор имеет следующий вид:
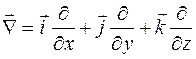 , (35.2)
, (35.2)
где 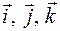 – орты координатных осей. В результате действия оператора Гамильтона на функцию
– орты координатных осей. В результате действия оператора Гамильтона на функцию  получается новая векторная функция
получается новая векторная функция 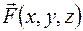 , причем проекции вектора
, причем проекции вектора 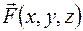 в каждой точке с координатами
в каждой точке с координатами  равны частным производным от исходной функции
равны частным производным от исходной функции  по соответствующей координате:
по соответствующей координате:
 . (35.3)
. (35.3)
Оператор Гамильтона можно представить в виде символического вектора, "проекциями" которого на координатные оси является оператор дифференцирования по соответствующей координате. Такое представление оператора с учетом правил векторной алгебры делает более удобным его использование в математических выкладках.
Пример 1
Умножение вектора 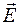 на число k сводится, как известно, к умножению проекций этого вектора на k. Тогда выражение (35.3) можно представить как результат умножения "вектора"
на число k сводится, как известно, к умножению проекций этого вектора на k. Тогда выражение (35.3) можно представить как результат умножения "вектора" 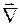 на "число" f. При этом "умножение" означает подстановку функции f в дифференциальный оператор. Правая часть выражения (35.3) есть градиент функции f, поэтому можно записать
на "число" f. При этом "умножение" означает подстановку функции f в дифференциальный оператор. Правая часть выражения (35.3) есть градиент функции f, поэтому можно записать
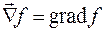 . (35.4)
. (35.4)
В частности, если под функцией f понимать потенциал электрического поля, то связь напряженности 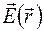 с потенциалом
с потенциалом 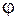 можно выразить следующим образом:
можно выразить следующим образом:
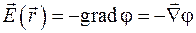 . (35.5)
. (35.5)
Пример 2
Скалярное произведение векторов  и
и 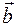 равно
равно 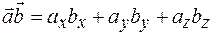 . С учетом этого дивергенцию вектора
. С учетом этого дивергенцию вектора 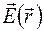 можно представить как скалярное произведение векторов
можно представить как скалярное произведение векторов 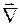 и
и 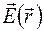 , т. е.
, т. е.
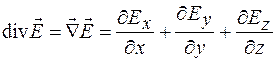 . (35.6)
. (35.6)
Пример 3
Векторное произведение векторов выражается определителем третьего порядка
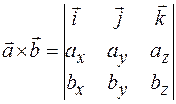 .
.
Легко показать, что ротор вектора 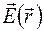 , определяемый выражением (34.3), можно представить в виде векторного произведения
, определяемый выражением (34.3), можно представить в виде векторного произведения 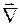 и
и 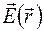 :
:
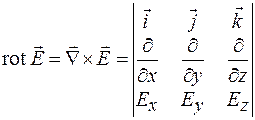 . (35.7)
. (35.7)
Пример 4
Если оператор Гамильтона "умножить" скалярно сам на себя, то получится новый оператор, называемый оператором Лапласа:
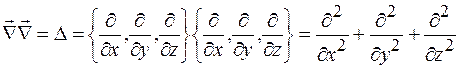 . (35.8)
. (35.8)
Используя оператор Лапласа, волновое уравнение (25.2) можно записать в следующем виде:
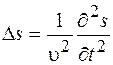 . (35.9)
. (35.9)
Пример 5
Составим двойное векторное произведение оператора Гамильтона и вектора 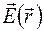 :
:
 .
.
Из примера 3 следует, что его можно представить как ротор ротора вектора 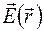 , т. е.
, т. е. 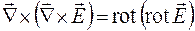 . Для двойного векторного произведения справедливо равенство
. Для двойного векторного произведения справедливо равенство 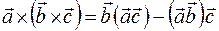 . С учетом этого можно записать
. С учетом этого можно записать
 .
.
Используя рассмотренные выше примеры, получим
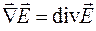 ,
,
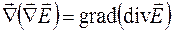 ,
,
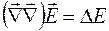
и окончательно можно записать
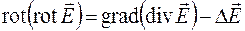 . (35.10)
. (35.10)
Полученное выражение потребуется в дальнейшем для анализа уравнений Максвелла.
Дата добавления: 2015-08-08; просмотров: 2231;
