В дифференциальной форме

 Очевидно, что в любой точке внутри потока жидкость не возникает и не исчезает, поэтому можно считать что в любой точке должны выполняться определённые соотношения, содержащие скорость и выражающие закон сохранения массы. Для вывода уравнения такого рода представим внутри потока воображаемую неподвижную замкнутую поверхность, через которую может свободно протекать жидкость. Положительное направление нормали ориентировано внутрь поверхности, рис. 7.1. Любой бесконечно малый элемент
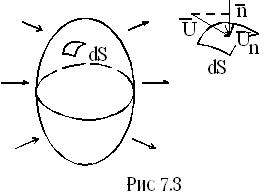
Очевидно, что в любой точке внутри потока жидкость не возникает и не исчезает, поэтому можно считать что в любой точке должны выполняться определённые соотношения, содержащие скорость и выражающие закон сохранения массы. Для вывода уравнения такого рода представим внутри потока воображаемую неподвижную замкнутую поверхность, через которую может свободно протекать жидкость. Положительное направление нормали ориентировано внутрь поверхности, рис. 7.1. Любой бесконечно малый элемент 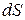 этой поверхности, ввиду его малости можно рассматривать как плоскую площадку и скорость в её пределах считать неизменной. Кроме того, на каждой площадке определён вектор нормали
этой поверхности, ввиду его малости можно рассматривать как плоскую площадку и скорость в её пределах считать неизменной. Кроме того, на каждой площадке определён вектор нормали 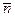 к ней. Составим для каждого элемента поверхности
к ней. Составим для каждого элемента поверхности 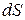 произведение
произведение
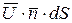 ,
,
которое можно представить как
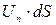 ,
,
где 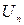 – проекция скорости на нормаль к площадке. Последнее произведение является, по определению, расходом жидкости через площадку
– проекция скорости на нормаль к площадке. Последнее произведение является, по определению, расходом жидкости через площадку 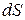 ,т. е.
,т. е.
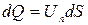 .
.
Припишем величине 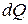 знаки (-) или (+) в зависимости от направления векторов
знаки (-) или (+) в зависимости от направления векторов 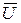 и
и  (противоположные или одноимённые), т.е. втекает жидкость внутрь поверхности (+) или вытекает из неё наружу (-). Если рассматривать однородную несжимаемую жидкость, то объём втекающей внутрь поверхности жидкости за любой промежуток времени равен объёму жидкости, вытекающей из неё. Суммарный расход через поверхность тогда, очевидно, будет равен нулю, т. е.
(противоположные или одноимённые), т.е. втекает жидкость внутрь поверхности (+) или вытекает из неё наружу (-). Если рассматривать однородную несжимаемую жидкость, то объём втекающей внутрь поверхности жидкости за любой промежуток времени равен объёму жидкости, вытекающей из неё. Суммарный расход через поверхность тогда, очевидно, будет равен нулю, т. е.
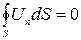 . (7.1)
. (7.1)
Применяя теорему Гаусса-Остроградского к рассматриваемой замкнутой поверхности 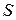 , получим
, получим
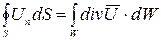 . (7.2)
. (7.2)
Подставляя (7.1) в (7.2) получим
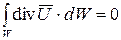 . (7.3)
. (7.3)
Так как поверхность 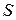 была выбрана произвольно и никаких ограничений сделано не было, то из (7.3) следует, что
была выбрана произвольно и никаких ограничений сделано не было, то из (7.3) следует, что
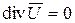 (7.4)
(7.4)
в каждой точке объёма 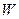 .
.
В декартовой системе координат зависимость (7.4) будет иметь вид
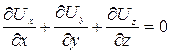 . (7.5)
. (7.5)
Уравнение (7.5) представляет собой уравнение неразрывности в дифференциальной форме; оно должно выполняться в каждой точке потока несжимаемой жидкости и накладывает, таким образом, ограничения на компоненты 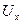 ,
,  и
и  вектора скорости. Заметим для сравнения, что при движении материальной точки (в классической механике) никаких ограничений на её скорость не накладывается, в то время как в любой точке потока несжимаемой жидкости такое ограничение существует в виде уравнения (7.5).
вектора скорости. Заметим для сравнения, что при движении материальной точки (в классической механике) никаких ограничений на её скорость не накладывается, в то время как в любой точке потока несжимаемой жидкости такое ограничение существует в виде уравнения (7.5).
Задача 7.1. Может ли существовать поток несжимаемой жидкости, поле скорости которого описывается вектором 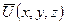 с компонентами
с компонентами
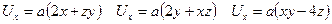 ,
,
где 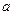 – постоянный коэффициент, введённый, в частности, для сохранения размерности скорости?
– постоянный коэффициент, введённый, в частности, для сохранения размерности скорости?
Решение. В каждой точке потока несжимаемой жидкости обязательно должно выполняться уравнение неразрывности (7.5). Вычислим частные производные
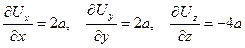 .
.
Следовательно, в данном случае уравнение неразрывности выполняется в каждой точке и поток с заданными компонентами скорости существует.
Дата добавления: 2015-08-01; просмотров: 1433;
