То поток называется вихревым.

Для вычисления вектора 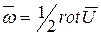удобно использовать символический определитель

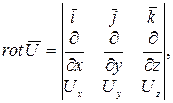(9.3)

который раскладывается по элементам первой строки, т.е. по ортам

В результате искомый вектор вихря(ротора) примет такой вид

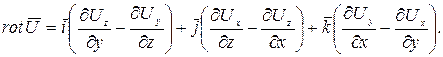(9.4)

Проекции вектора 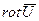на оси декартовой системы координат равны

2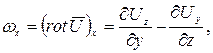

2 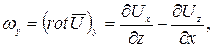(9.5)

2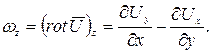

Задача 9.1. Определить, вихревым или безвихревым является течение, заданное вектором скорости с компонентами

,

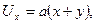
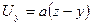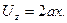
(а – постоянная, имеющая размерность 1/t).

Решение. Прежде всего необходимо убедиться, что поток ,заданный такими компонентами скорости, существует. Для этого подставляем значения U_x, U_y, U_z из условия задачи в уравнение неразрывности (7.5) и убеждаемся , что оно удовлетворяется. Далее подставляем U_x, U_y, U_z из условия задачи в (9.3) и находим

Течение является вихревым, так как вектор вихря не равен нулю.

Если поток является безвихревым и выполняется условие 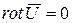, то существует скалярная функция координат и времени , обладающая свойством: частная производная от этой функции по какому-либо направлению равна проекции скорости на это же направление. Частную производную от функции 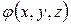по любому направлению 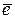можно найти, умножив скалярно градиент от этой функции на вектор 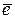, т.е.

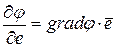. (9.6)

В прямоугольной системе координат это записывается так

,

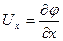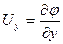, (9.7)

.

Функция φ(x¸y¸z) называется потенциалом скорости. Поэтому безвихревое движение жидкости называется также потенциальным. Предположение о том, что

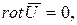
т.е. движение является потенциальным, приводит к значительным упрощениям при получении аналитических решений, а именно вместо трёх неизвестных величин 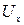, , 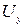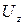возможно с помощью (9.7) свести задачу об определении поля скоростей к нахождению одной неизвестной функции.

Примерами потоков, для которых допущение о потенциальности оказывается не только возможным, но и полезным для их изучения, являются: 1. Различные случаи истечения из отверстий; 2. Водосливы; 3. Закругления трубопроводов; 4. Течения в затворах шлюзов; 5. Фильтрационные потоки в пористой среде. К приведённым примерам необходимо добавить важный класс явлений обтекания различных препятствий потоками жидкости и газа. Функция потенциала скорости может быть введена для трёхмерных и двумерных (плоских) потоков. Любой поток идеальной жидкости может быть или вихревым, или потенциальным. Следует иметь также в виду, что все течения жидкости, существующие в природе, являются вихревыми; известна теорема, согласно которой, если жидкость неидеальная (вязкая), то никакое её движение не может быть потенциальным. Течение идеальной жидкости, таким образом, может быть как потенциальным, так и вихревым, течение же вязкой жидкости всегда может быть только вихревым.

В заключение заметим, что поле скоростей потока в случае, когда движение происходит без вращения частиц, обладает свойствами, аналогичными свойствам поля силы, имеющей потенциал. В том и другом случаях интеграл от дифференциального выражения вида

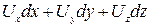
не зависит от формы пути интегрирования, а зависит лишь от координат начальной А и конечной В точек пути

.

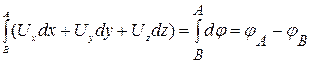Поэтому было предложено называть функцию 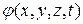потенциалом скоростей.

Задача 9.2. Доказать, что если выполняются условия (9.7), то течение является безвихревым.

Указание. Подставить выражения для U_x, U_y, U_z из (9.7) в зависимости для ω_x, ω_y, ω_z и убедиться, что все три составляющие ω_x, ω_y, ω_z становятся равными нулю.