Общий характер движения жидкой частицы
Жидкость обладает свойством текучести и является легко деформируемой средой, пример – трансформация жидкой капли при растекании её по твёрдой поверхности. Напомним, что твёрдое тело может участвовать одновременно в поступательном движении и во вращательном. Одной из характеристик интенсивности вращательного движения является угловая скорость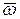 
. Если известно поле скоростей 
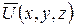, то возможно определить вектор 
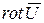(ротор вектора скорости), связанный с вектором угловой скорости 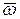так
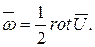
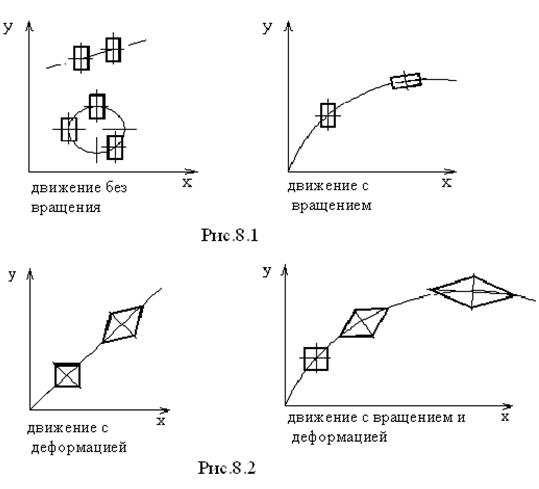
Помимо вращательного движения жидкая частица может деформироваться, и для каждой её точки это будет эквивалентно участию в так называемом деформационном движении. Все возможные виды наглядно изображены на рис. 8.1 и 8.2.
Основная теорема кинематики жидкости – первая теорема Коши-Гельмгольца – этот результат формулирует так: скорость любой точки жидкой частицы складывается из скорости полюса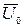 
, скорости при вращении вокруг мгновенной оси, проходящей через полюс 
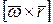, и скорости деформационного движения 
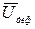. Обозначим составляющие поступательной скорости полюса 
, 
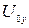и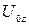 
, составляющие вектора угловой скорости полюса 
, 
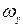и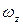 
, составляющие скорости деформации Uxдеф, Uyдеф и Uzдеф. Тогда возможно выразить проекции скоростей движения в любой точке потока. Например,
.
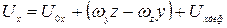Задача 8.1.Выразить проекцию скорости 
через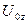 
, 
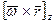и Uzдеф.
Дата добавления: 2015-08-01; просмотров: 1165;