Изменение скорости вдоль потока
Жидкости по-разному взаимодействуют с поверхностью, с которой они соприкасаются. Например, вода прилипает к чистой поверхности стекла или, как говорят, смачивает стекло. Однако та же вода не смачивает стекло, покрытое слоем жира или масла; ртуть не смачивает стекло. Так как обычно используют металлические трубопроводы, а в открытых каналах стенки земляные или бетонные, по которым подают обычные жидкости – воду, жидкие топлива, нефть – везде в дальнейшем считаем, что поверхность трубы смачивается текущей в ней жидкостью. При смачивании тончайший слой жидкости, непосредственно соприкасающейся со стенкой, как бы прилипает к ней и, следовательно, при общем движении жидкости фактически остаётся неподвижным. По этому слою медленно скользит следующий слой, по нему, чуть быстрее, другой слой, по тому, ещё быстрее, третий и т.д. Таким образом, скорость жидкости, по мере перехода от каждого слоя к следующему, нарастает, достигая максимума в центре сечения трубы или на поверхности открытого канала. Такое представление удобно для начального понимания гидравлических закономерностей; в действительности отдельных слоёв жидкости не существует и скорость изменяется непрерывно. Закон изменения скорости по сечению трубы зависит от режима движения и во многих случаях очень сложен. Для решения большинства задач гидравлики достаточно знать среднюю скорость потока 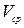 однозначно определяющую расход и многие другие гидравлические величины. Для нахождения
однозначно определяющую расход и многие другие гидравлические величины. Для нахождения 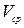 усредним скорость по всей площади сечения (т.е. выполним обычную операцию усреднения). При этом средняя скорость определяется так
усредним скорость по всей площади сечения (т.е. выполним обычную операцию усреднения). При этом средняя скорость определяется так
 (6.1)
(6.1)
Из (6.1) следует, что
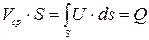 . (6.2)
. (6.2)
Таким образом, средняя скорость определяется как частное величин Q и S (в дальнейшем 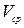 будем обозначать как V)
будем обозначать как V)
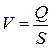 . (6.3)
. (6.3)
Уравнение (5.2) можно теперь записать так
 , (6.4)
, (6.4)
а уравнение постоянства массового расхода
 . (6.5)
. (6.5)
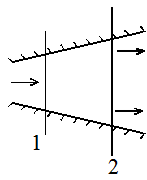
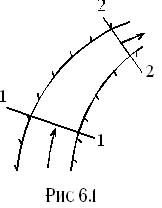 Выберем два любых сечения 1 и 2 в потоке, рис. 6.1, тогда для расходов Q1 и Q2 в них
Выберем два любых сечения 1 и 2 в потоке, рис. 6.1, тогда для расходов Q1 и Q2 в них
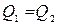
или
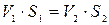 . (6.6)
. (6.6)
Если уравнение неразрывности записать для нескольких сечений, то оно будет иметь вид

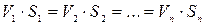 . (6.7)
. (6.7)
Пример 6.1. Представим, что поставлена задача определить среднюю скорость V воды в водопроводной трубе диаметром d = 15 мм при полном открытии крана. Среднюю скорость определим по формуле
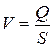
и поэтому вначале измерим расход воды объёмным способом. В процессе измерения набрали в мерную ёмкость 2,7 литра за 15 секунд и определили расход по формуле
 .
.
Затем определили среднюю скорость V
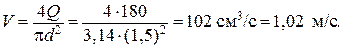
Замечание 6.1. Для потока, изображенного на рис.6.1, вопрос «в каком сечении расход больше – в узком или широком?» не имеет смысла, так как расход согласно (6.4) в любом сечении одинаковый, чего нельзя сказать о средней скорости. Очевидно, что если Q=const, то и 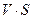 =const: поэтому где площадь сечения больше, там скорость меньше и наоборот.
=const: поэтому где площадь сечения больше, там скорость меньше и наоборот.
Замечание 6.2. Зависимости (5.2), (6.4), (6.6) и (6.7) являются различными формами записи уравнения неразрывности для потока и применимы к его осреднённым характеристикам. Равенство (6.6), основываясь на свойстве пропорции, возможно представить так

Из него следует, что отношение средних скоростей обратно пропорционально отношению площадей. Для круглой трубы площадь сечения  и поэтому скорости в сечениях относятся обратно пропорционально квадратам диаметров.
и поэтому скорости в сечениях относятся обратно пропорционально квадратам диаметров.
Пример 6.2. а) Если диаметр трубы увеличить в 2 раза, то средняя скорость в этом сечении уменьшится в 4 раза; б) если диаметр трубы в данном сечении уменьшить в 3 раза, то средняя скорость в этом сечении увеличится в 9 раз.
Задача 6.1. Определить массовый расход горячей воды в трубопроводе с внутренним диаметром  , если известно, что средняя скорость воды
, если известно, что средняя скорость воды  , а плотность r = 920 кг/м3.
, а плотность r = 920 кг/м3.
Решение. Массовый расход определяем по формуле
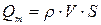 .
.
Площадь живого сечения равна
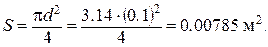
окончательно
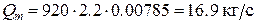
Задача 6.2. Скорость 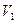 в сечении 1 круглой трубы диаметром
в сечении 1 круглой трубы диаметром  равна
равна
 ; найти скорость
; найти скорость  в сечении 2 при расширении трубы. Диаметр
в сечении 2 при расширении трубы. Диаметр 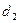 во втором сечении в 3 раза больше, чем диаметр в сечении 1.
во втором сечении в 3 раза больше, чем диаметр в сечении 1.
Решение.Расход в обоих сечениях одинаковый и согласно уравнению (5.6) имеем
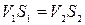 .
.
Подставляя в последнее равенство выражения для площади сечения, получим

 или
или 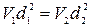 .
.
Последнее равенство можно представить в виде
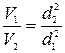 ,
,
т.е. скорости обратно пропорциональны квадратам диаметров. Подставляя числовые значения, получим окончательно
 .
.
Дата добавления: 2015-08-01; просмотров: 4309;
