Для элементарной струйки

Известно несколько общих законов природы – законов сохранения, которые, преломляясь в прикладных науках, остаются в них определяющими. В гидравлике одним из основных уравнений является уравнение неразрывности, выражающее один из фундаментальных законов природы – закон сохранения массы вещества применительно к движению жидкостей и газов.

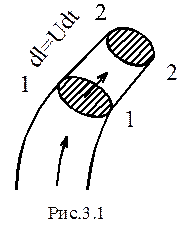Для вывода этого уравнения рассмотрим элементарную струйку и определим массу жидкости, протекающей в единицу времени через её сечение. (1-1, рис. 3.1). Выражение для элементарной массы составим следующим образом: за время 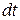все частицы жидкости из сечения 1-1 переместятся на расстояние 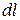, равное 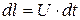, и займут положение на плоской площадке 2-2, которая не является сечением элементарной струйки, а представляет основание цилиндра, построенного на сечении 1-1 с образующей, равной 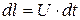, где U-скорость в сечении струйки 1-1. Ввиду того, что площадь сечения струйки является бесконечно малой величиной, скорость в его пределах полагается постоянной. Поэтому за время 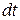через сечение 1-1 протекает масса жидкости, содержащаяся в цилиндре, рис. 3.1, ограниченном с торцов сечениями 1-1 и 2-2, а боковая его поверхность образована линиями тока. Эта масса может быть определена как объем цилиндра, умноженный на плотность жидкости

. (3.1)

За единицу времени через сечение 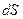протекает масса жидкости

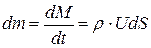. (3.2)

Поверхность струйки непроницаема для жидкости и поэтому для данной струйки имеем

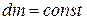, (3.3)

или

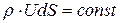. (3.4)

По длине струйки площадь её сечения может изменяться, но произведение (3.4) остается постоянным, т. е. масса жидкости, проходящая в единицу времени через любое сечение струйки, остается постоянной –так формулируется закон сохранения массы для данного случая.

Если жидкость несжимаема, то и (3.4) будет иметь вид

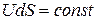. (3.5)

Произведение 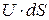называется объемным расходом. В дальнейшем, если не сделана оговорка, под расходом будем понимать объемный расход.