Ускорение жидкой частицы
Вектор ускорения жидкой частицы, движущейся со скоростью  , по аналогии с механикой материальной точки, является производной по времени от вектора скорости
, по аналогии с механикой материальной точки, является производной по времени от вектора скорости
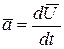 . (2.1)
. (2.1)

 Выполним вначале качественный анализ зависимости для ускорения жидкой частицы. В данной точке потока скорость может со временем изменяться
Выполним вначале качественный анализ зависимости для ускорения жидкой частицы. В данной точке потока скорость может со временем изменяться 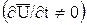 , а может и оставаться постоянной
, а может и оставаться постоянной 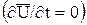 ; это относится к любой точке и частная производная
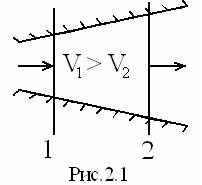
; это относится к любой точке и частная производная  (имеющая размерность ускорения) будет первой составляющей (слагаемым) компоненты ускорения. Кроме того, скорость частицы может изменяться от точки к точке (как при стационарном, так и при нестационарном режимах); простейший пример – течение жидкости в расширяющемся канале, рис. 2.1, где скорость непрерывно уменьшается вдоль потока. В этой второй составляющей ускорения по смыслу должны присутствовать производные от скорости по координатам, но для сохранения размерности ускорения они должны умножаться на скорость. Так как обе рассматриваемые компоненты принципиально независимы, то общее ускорение жидкости частицы состоит из двух слагаемых.
(имеющая размерность ускорения) будет первой составляющей (слагаемым) компоненты ускорения. Кроме того, скорость частицы может изменяться от точки к точке (как при стационарном, так и при нестационарном режимах); простейший пример – течение жидкости в расширяющемся канале, рис. 2.1, где скорость непрерывно уменьшается вдоль потока. В этой второй составляющей ускорения по смыслу должны присутствовать производные от скорости по координатам, но для сохранения размерности ускорения они должны умножаться на скорость. Так как обе рассматриваемые компоненты принципиально независимы, то общее ускорение жидкости частицы состоит из двух слагаемых.
Выполним теперь формальный вывод зависимости для ускорения. В общем случае неустановившегося движения проекции скорости  ,
, 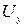 ,
,  являются функциями координат и времени; поэтому полный дифференциал, например, проекции
являются функциями координат и времени; поэтому полный дифференциал, например, проекции  равен
равен
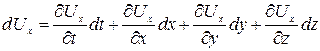 . (2.2)
. (2.2)
Разделив последнее равенство на  , получим
, получим
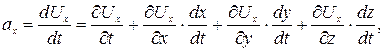 (2.3)
(2.3)
а с учетом
 ,
, 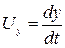 ,
, 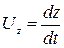 (2.4)
(2.4)
получим
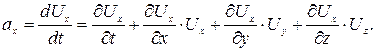 (2.5)
(2.5)
Из анализа последней зависимости следует, что полное ускорение  складывается из двух составляющих: конвективного (или переносного) ускорения
складывается из двух составляющих: конвективного (или переносного) ускорения
 (2.6)
(2.6)
и местного (локального) ускорения
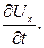 (2.7)
(2.7)
Как следует из вывода, местное ускорение  – это результат изменения скорости в точках пространства с течением времени, т. е. когда движение жидкости является неустановившимся. При установившемся движении местное ускорение
– это результат изменения скорости в точках пространства с течением времени, т. е. когда движение жидкости является неустановившимся. При установившемся движении местное ускорение  .
.
Возникновение конвективного ускорения
 (2.8)
(2.8)
обусловлено тем, что при переходе от точки к точке скорость изменяется. Таким образом, конвективное ускорение, а следовательно, и полное ускорение в установившемся потоке не обязательно равно нулю.
Задача 2.1. В каком случае конвективное ускорение равно нулю во всех точках потока?
Задача 2.2. Заданы выражения для компонентов вектора скорости
 ,
,  ,
,  ,
,
где  – постоянная величина, имеющая размерность
– постоянная величина, имеющая размерность 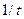 ;
; 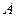 ,
,  ,
, 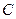 – постоянные, имеющие размерность скорости. Найти выражение для компоненты
– постоянные, имеющие размерность скорости. Найти выражение для компоненты  вектора ускорения.
вектора ускорения.
Задача 2.3. Заданы следующие выражения ля компонентов вектора скорости течения
 ,
, 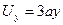 ,
,  ,
,
где  – постоянная величина, имеющая размерность
– постоянная величина, имеющая размерность 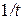 . Найти выражение для компоненты
. Найти выражение для компоненты 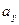 вектора ускорения.
вектора ускорения.
Решение. Выражение для компоненты ускорения 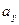 имеет вид
имеет вид
 .
.
Из условия задачи следует
 ,
, 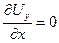 ,
, 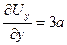 ,
,  .
.
Подставляя полученные значения производных и выражения для компонент 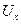 ,
, 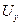 и
и  в зависимость для
в зависимость для 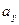 , получаем искомый результат
, получаем искомый результат
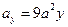 .
.
Дата добавления: 2015-08-01; просмотров: 2341;
