Вопрос №32. Движение частицы по поверхности лопасти ротора.

Анализируя рабочий процесс взаимодей­ствия ротора со снегом, можно выделить следующие операции: захват снега лопастью; пере­мещение снега вдоль лопасти; движение снега по кожуху ротора к выбросному отвер­стию; движение снега по на­правляющему устройству.

Для упрощения математи­ческого описания рабочего про­цесса в роторе исключены силы взаимодействия между отдель­ными частицами снега и анали­зируется поведение отдельно взятой материальной частицы на прямолинейной лопасти с мо­мента ее поступления на лопасть до момента, когда частица достигла края лопасти.

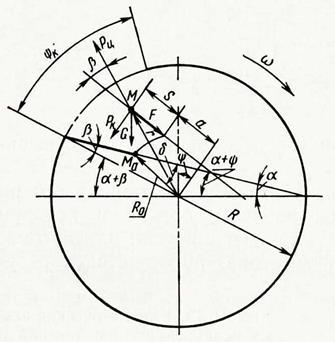
Рис. 26. Схема сил, приложенных к материальной частице, движущейся по вращающейся лопасти ротора.

В наиболее общем случае лопасть расположена в роторе под некоторым произвольным углом β к радиусу R (рис. 26), а угловая скорость вращения ротора

ω = const.

Пусть начальное положение лопасти с горизонтальной осью ротора в момент ее подхода к выбросному отверстию определяется углом α, а начальное положение рассматриваемой частицы М₀на лопасти — радиусом R₀. Так как ротор вращается с постоян­ной угловой скоростью, то за отрезок времени t лопасть повернется вокруг оси ротора на угол ψ = ωt, а частица перейдет в точку М, определяемую радиусом r, и, двигаясь по лопасти со скоростью v_отн, пройдет за это иремя путь

.

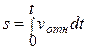Лопасть к этому моменту займет положение, определяемое углом наклона ее к горизонту (α + ψ).

На рассматриваемую частицу массой т, расположенную в точке М, действуют сила тяжести G, центробежная сила Р_ц, кориолисова сила инерции Р_ки сила трения F, вызываемая силой тяжести, кориолисовой силой инерции и центробежной силой.

Обозначив через а расстояние от начального положения ча­стицы до перпендикуляра, опущенного на лопасть из центра вращения ротора, и спроектировав все силы, приложенные к ча­стице, на направление лопасти, получим уравнение динамического равновесия частицы в следующем виде:

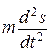= Р_ц.т.- Gsin(α + ψ) - F,(1)

где Р_ц.т. — проекция центробежной силы инерции на направление лопасти; Р_ц.т. = тω² (α+ s); F — сила трения; F = μ₁ [Р_к + G cos (α + ψ) — Р_ц.н.] (здесь μ₁ = tg ρ₀ — коэффициент внешнего трения; Р_ц.н. — проекция центро­бежной силы на нормаль к лопасти; Р_ц._н = mω²R sin β).

После подстановки значений Р_ц.т., F, Р_ц.н. в выражение (1) и t = ψ/ω, а также сокращения всех членов на массу, полу­чаем неоднородное линейное дифференциальное уравнение вто­рого порядка

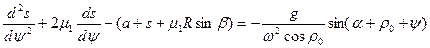. (2)

Обозначив а + s + μ₁R sin β = х, дифференциальное урав­нение примет следующий вид:

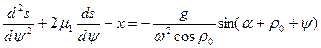(3)

Решая дифференциальное уравнение, получаем

х = 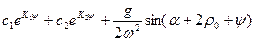. (4)

Таким образом, путь s, пройденный частицей по лопасти за время t, и относительная скорость частицы v_отн за время t

s = 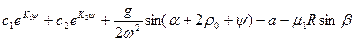_; (5)

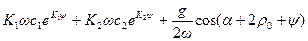v_отн= . (6)

Используя граничные условия (при t = 0, s = 0 и v_oтн= 0), находим произвольные постоянные

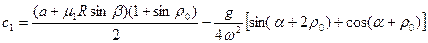; (7)

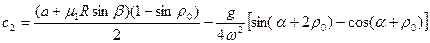; (8)

Так как а = R cos δ и R₀sin δ = R sin β, то

а + μ₁R sin β = R₀ (cos δ + μ₁sinδ) = R₀ cos (ρ₀ — δ) cos ρ₀.

Следовательно,

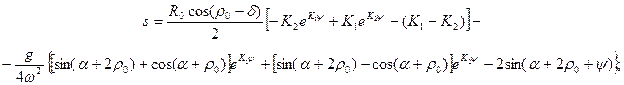(9)

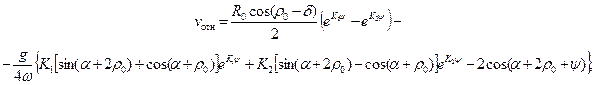(10)

где К₁ = 1 — sin ρ₀/cos ρ₀; К₂= — (1 + sin ρ₀)/cos ρ₀

Выражения (9) и (10) определяют характер движения частицы по лопасти в общем случае, когда учтены все силы, приложенные к частице, и наружный край лопасти по ходу вра­щения ротора откинут назад. Очевидно, что когда он закинут вперед, знак перед δ должен быть заменен на обратный, а для радиальной лопасти

δ = 0.

Для упрощения полученных выражений, а также учитывая малую силу тяжести частицы снега по сравнению с силами инер­ции, принимают G = 0, и выражения (9) и (10) будут иметь вид

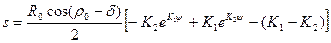; (11)

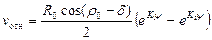. (12)

Из приведенных выражений можно определить конечную относительную скорость частицы v_отн.к , если вместо s подставить его значение

s_к = R cos β — R₀ cos δ, соответствующее ψ= ψ_к.

При радиальном расположении лопастей роторов р = 0 и δ = 0, и конечная относительная скорость определяется из усло­вия s = R — R₀.

Так как cos ρ₀/2 = l/( К₁ — К₂), то из выражений (11) и (12) получаем, что при радиальном расположении лопастей

R= 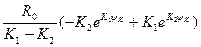;(13)

v_отн.к = 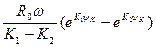;(14)

Абсолютная скорость частицы v_а на выходе из ротора, равная геометрической сумме относительной v_отн.к и переносной ско­рости v_пер, в общем случае

v_a= 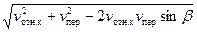. (15)

При радиальном расположении лопастей

v_a= ,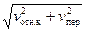

где v_пер = ωR— окружная скорость лопасти.