Вращательное движение твердого тела. Угловая скорость и ускорение, их связь с линейными величинами
В случае движения материальной точки по окружности по аналогии с линейными скоростью и ускорением вводятся угловая скорость и угловое ускорение.
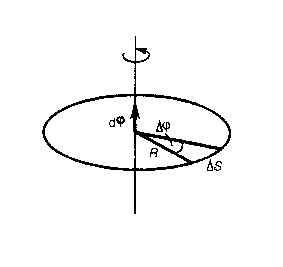 Рис. 6
Рис. 6
| Пусть точка движется по окружности радиуса R (рис.6). Ее положение через малый промежуток времени зададим углом  . Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: . Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
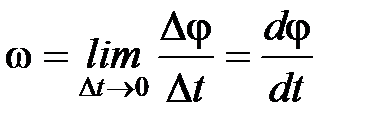 . .
|
Направление вектора угловой скорости задается правилом винта: вектор угловой скорости совпадает по направлению с поступательным движением острия винта, головка которого вращается в направлении движения точки по окружности (рис. 7).
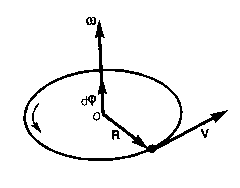 Рис.7
Рис.7
| Размерность угловой скорости [ 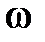 ]=с ]=с 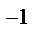 , а ее единица - радиан в секунду (рад/с). Линейная скорость точки (см. рис. 1) , а ее единица - радиан в секунду (рад/с). Линейная скорость точки (см. рис. 1)
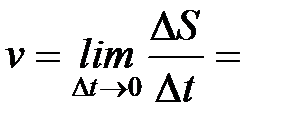 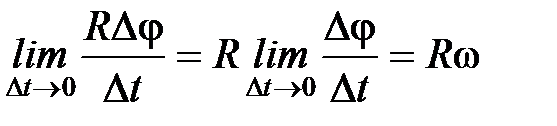 . .
|
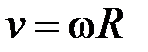 .
.
Если  = const, то вращение равномерное и его можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2
= const, то вращение равномерное и его можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2 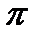 . Так как промежутку времени
. Так как промежутку времени 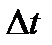 = Т соответствует
= Т соответствует 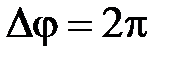 , то
, то 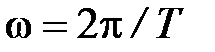 , откуда
, откуда
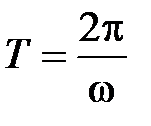 .
.
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:
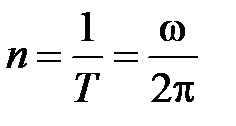 , откуда
, откуда  .
.
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
 .
.
Из этой формулы следует, что вектор углового ускорения направлен по оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор  параллелен вектору
параллелен вектору 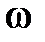 (рис. 8), при замедленном — антипараллелен (рис. 9).
(рис. 8), при замедленном — антипараллелен (рис. 9).
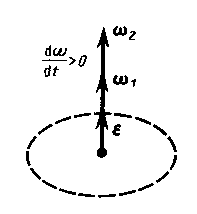 Рис. 8
Рис. 8
| 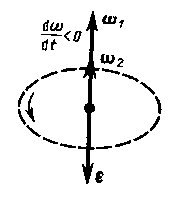 Рис. 9
Рис. 9
|
Тангенциальная составляющая ускорения 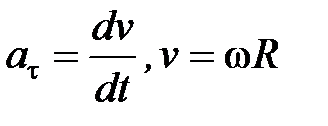 и
и
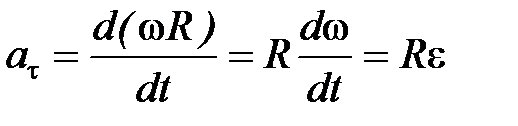
Нормальная составляющая ускорения
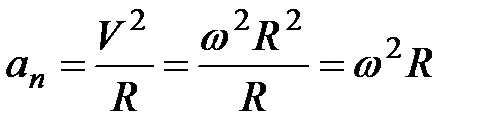 .
.
Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение  нормальное ускорение
нормальное ускорение 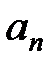 и угловыми величинами (угол поворота
и угловыми величинами (угол поворота 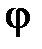 , угловая скорость
, угловая скорость 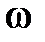 , угловое ускорение
, угловое ускорение  выражается следующими формулами:
выражается следующими формулами:
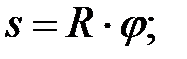
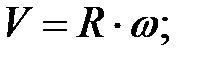
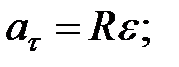
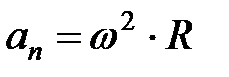
В случае равнопеременного движения точки по окружности (e = const)

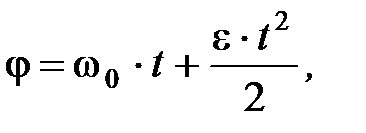 где w0 – начальная угловая скорость.
где w0 – начальная угловая скорость.
Дата добавления: 2015-08-11; просмотров: 2751;
