Ускорение и его составляющие
В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.
Пусть вектор 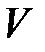 задает скорость точки А в момент времени
задает скорость точки А в момент времени 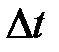 . За время
. За время 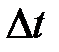 движущаяся точка перешла в положение В и приобрела скорость, отличную от v как по модулю, так и направлению, равную
движущаяся точка перешла в положение В и приобрела скорость, отличную от v как по модулю, так и направлению, равную 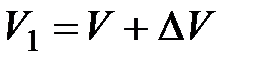 . Перенесем вектор
. Перенесем вектор  в точку А и найдем
в точку А и найдем 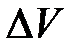 (рис. 4).
(рис. 4).
Средним ускорением неравномерного движения в интервале от  до
до 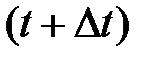 называется векторная величина, равная отношению изменения скорости
называется векторная величина, равная отношению изменения скорости 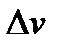 к интервалу времени
к интервалу времени 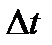 :
:
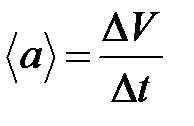
 Рис.4
Рис.4
| Мгновенным ускорением  материальной точки в момент времени материальной точки в момент времени  будет предел среднего ускорения: будет предел среднего ускорения:
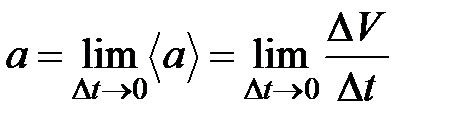 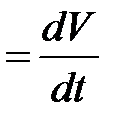 .
Таким образом, ускорение .
Таким образом, ускорение  есть векторная величина, равная первой производной скорости по времени.
Разложим вектор есть векторная величина, равная первой производной скорости по времени.
Разложим вектор 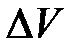 на две составляющие. Для этого из точки А (см. рис. 4) по направлению скорости v отложим вектор AD, по модулю равный на две составляющие. Для этого из точки А (см. рис. 4) по направлению скорости v отложим вектор AD, по модулю равный 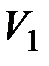  . .
|
Очевидно, что вектор CD, равный 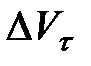 представляет собой изменение скорости по модулю за время
представляет собой изменение скорости по модулю за время 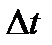 :
:
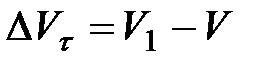 .
.
Вторая же составляющая вектора 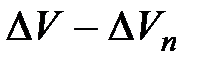 , характеризует изменение скорости за время
, характеризует изменение скорости за время 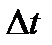 по направлению.
по направлению.
Предел отношения- 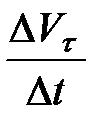 , являющийся производной от скорости по времени, определяет быстроту изменения скорости в данный момент времени
, являющийся производной от скорости по времени, определяет быстроту изменения скорости в данный момент времени 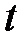 и является тангенциальной составляющей ускорения
и является тангенциальной составляющей ускорения 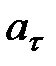 :
:
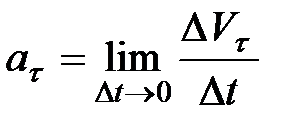
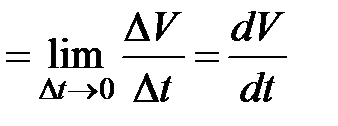 .
.
Определим вторую составляющую ускорения. Допустим, что точка 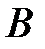 достаточно близка к точке
достаточно близка к точке 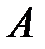 , поэтому
, поэтому 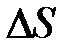 можно считать дугой окружности некоторого радиуса
можно считать дугой окружности некоторого радиуса 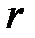 , мало отличающейся от хорды
, мало отличающейся от хорды 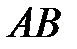 .. Тогда из подобия треугольников АОВ и EAD следует
.. Тогда из подобия треугольников АОВ и EAD следует 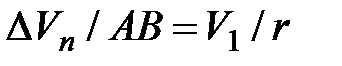 , но так как
, но так как  , то
, то

В пределе при 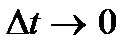
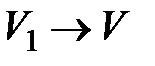 . Поскольку
. Поскольку  , угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол ADE между
, угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол ADE между 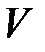 и
и 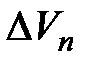 стремится к прямому. Следовательно, при
стремится к прямому. Следовательно, при  векторы
векторы 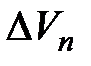 и
и 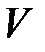 оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор
оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор 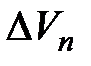 , перпендикулярный скорости, будет направлен к центру круга ее кривизны.
, перпендикулярный скорости, будет направлен к центру круга ее кривизны.
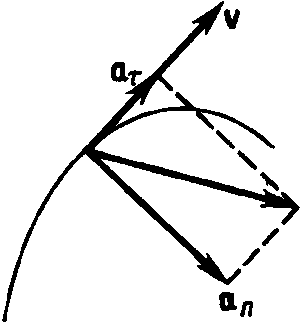 Рис. 5
Рис. 5
| Вторая составляющая ускорения, равная
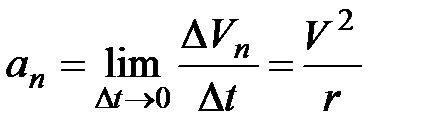 называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 5):
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 5):
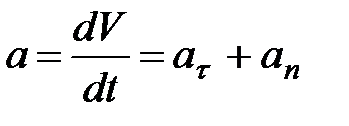 . .
|
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена к центру кривизны траектории).
С учетом тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом :
1) 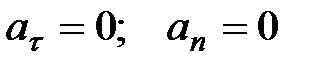 - прямолинейное равномерное движение;
- прямолинейное равномерное движение;
2) 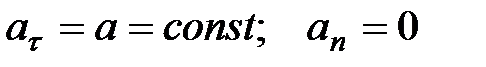 — прямолинейное равнопеременное движение. При таком виде движения
— прямолинейное равнопеременное движение. При таком виде движения
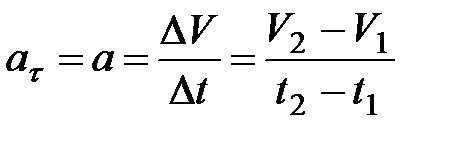 .
.
Если в начальный момент времени 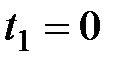 , а начальная скорость
, а начальная скорость 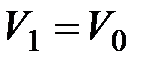
 , то, обозначив
, то, обозначив  и
и 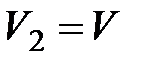 , получим
, получим 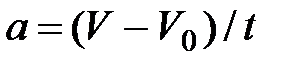 ,
,
откуда

Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, получим формулу для пройденного пути в случае равнопеременного движения:

3) 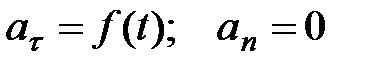 - прямолинейное движение с переменным ускорением;
- прямолинейное движение с переменным ускорением;
4) 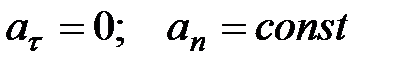 . При а
. При а 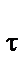 = 0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы
= 0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы 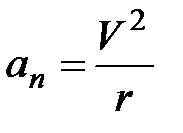 следует, что радиус кривизны должен быть постоянным. Следовательно, имеем дело с равномерным движением по окружности;
следует, что радиус кривизны должен быть постоянным. Следовательно, имеем дело с равномерным движением по окружности;
5) 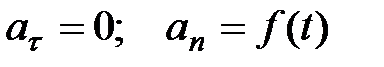 - равномерное криволинейное движение;
- равномерное криволинейное движение;
6) 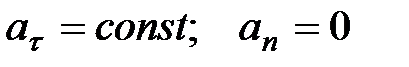 - криволинейное равнопеременное движение;
- криволинейное равнопеременное движение;
7) 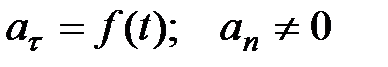 - криволинейное движение с переменным ускорением.
- криволинейное движение с переменным ускорением.
Дата добавления: 2015-08-11; просмотров: 2177;
