Движение частицы по окружности. Угловая скорость и угловое ускорение
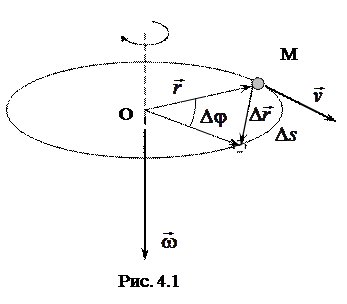 Пусть материальная точка М движется по окружности радиуса r, через центр которой (точка О) проходит ось вращения (рис. 4.1). За время Dt точка переместится по окружности на некоторое расстояние. При этом радиус-вектор
Пусть материальная точка М движется по окружности радиуса r, через центр которой (точка О) проходит ось вращения (рис. 4.1). За время Dt точка переместится по окружности на некоторое расстояние. При этом радиус-вектор 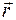 , проведенный из центра, повернется на угол
, проведенный из центра, повернется на угол 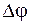 .
.
Средней угловой скоростью называется величина
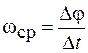 . (4.1)
. (4.1)
Мгновенная угловая скорость равна
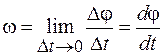 . (4.2)
. (4.2)
Вектор угловой скорости направлен вдоль оси вращения и связан с направлением движения точки правилом правого винта.
Единица угловой скорости - радиан на секунду ( 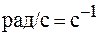 ).
).
Для линейной скорости движения точки по окружности находим
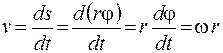 . (4.3)
. (4.3)
В векторной форме
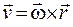 . (4.4)
. (4.4)
Если 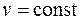 , то движение является равномерным. Для его описания используются величины:
, то движение является равномерным. Для его описания используются величины:
- период вращения Т - время одного оборота;
- частота вращения 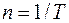 - число оборотов за единицу времени;
- число оборотов за единицу времени;
- полное число оборотов N,связано с углом поворота соотношением 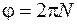 .
.
Из определения периода и угловой скорости следует, что
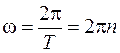 . (4.5)
. (4.5)
Если угловая скорость изменяется, то используется понятие углового ускорения
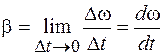 . (4.6)
. (4.6)
Если вектор угловой скорости сохраняет направление, а ее значение увеличивается, то 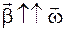 , если уменьшается, то
, если уменьшается, то 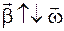 .
.
Единица углового ускорения - радиан на секунду в квадрате ( 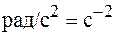 ). При наличии углового ускорения (
). При наличии углового ускорения ( 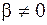 ) точка движется по окружности с тангенциальным
) точка движется по окружности с тангенциальным 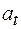 и центростремительным
и центростремительным 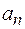 ускорениями (рис. 4.2).
ускорениями (рис. 4.2).
Тангенциальное ускорение 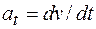 , а так как
, а так как 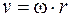 , то
, то
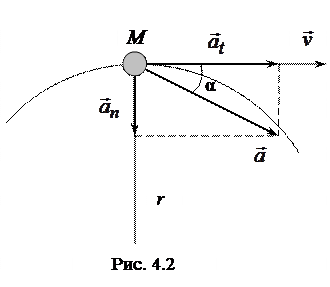
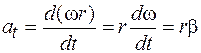 . (4.7)
. (4.7)
Нормальное ускорение
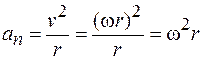 . (4.8)
. (4.8)
Из рисунка следует, что угол 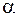 между векторами скорости и полного ускорения зависит от соотношения ускорений
между векторами скорости и полного ускорения зависит от соотношения ускорений 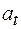 и
и 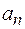 , так как
, так как 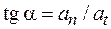 .
.
Дата добавления: 2015-08-08; просмотров: 5500;
