Определение положения точки в пространстве
При описании движения тел используют скалярные и векторные величины. Векторными называются величины, характеризующиеся численным значением и направлением. Скалярными называются величины, которые характеризуются только численным значением. Вектор изображается в виде стрелки, направление которой совпадает с направлением векторной величины, а длина стрелки в выбранном масштабе равна ее значению.
Законы природы, очевидно, должны быть записаны в форме, которая не зависит от выбора системы координат. Обычно используется прямоугольная (декартова) система. Положение точки в такой системе координат задается радиусом-вектором 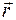 , проекции которого на оси координат равны соответственно
, проекции которого на оси координат равны соответственно 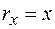 ,
, 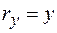 ,
, 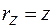 (рис. 2.1, а).
(рис. 2.1, а).
Таким образом, вектор 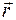 вполне однозначно определяется заданием трех его проекций, хотя это могут быть и другие три числа, например, длина r и два угла
вполне однозначно определяется заданием трех его проекций, хотя это могут быть и другие три числа, например, длина r и два угла 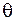 и
и 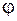 - так называемая сферическая система координат (рис. 2.1, б).
- так называемая сферическая система координат (рис. 2.1, б).
 |
Декартовы координаты со сферическими связаны соотношениями:
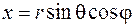 ,
,
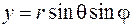 ,
,
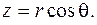
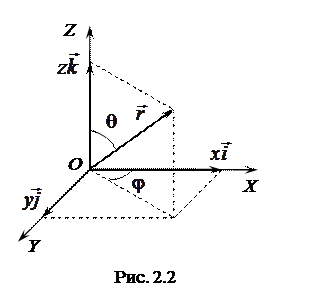 Используя единичные векторы
Используя единичные векторы 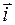 ,
, 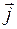 ,
, 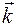 , направленные вдоль координатных осей (единичные орты), можно представить радиус-вектор
, направленные вдоль координатных осей (единичные орты), можно представить радиус-вектор 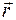 в виде суммы трех векторов:
в виде суммы трех векторов:
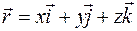 .
.
Сложение векторов осуществляется по правилу параллелограмма: слагаемые векторы являются сторонами параллелограмма, а результирующий вектор - его диагональю (рис. 2.2).
В соответствии с рисунком получим выражение для модуля радиуса-вектора через его проекции x, y, z:
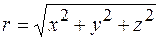 .
.
Дата добавления: 2015-08-08; просмотров: 1193;
