Кинематика твердого тела. При вращении твердого тела положение его точек относительно друг друга не меняется, все они движутся с одинаковыми угловыми скоростями и ускорениями по

При вращении твердого тела положение его точек относительно друг друга не меняется, все они движутся с одинаковыми угловыми скоростями и ускорениями по окружностям, центры которых лежат на оси вращения. Линейные скорости точек пропорциональны радиусам окружностей, по которым они движутся (4.3).

Получим кинематические уравнения для вращательного движения.

Из уравнения (4.6) находим 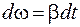. Проинтегрируем полученное выражение для случая :

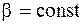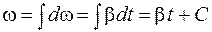. (5.1)

Постоянную интегрирования С определим, полагая, что при 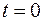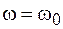. Это дает нам 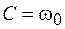. Подставляем в уравнение (5.1) и получаем

. (5.2)

При постоянном угловом ускорении угловая скорость линейно изменяется с течением времени.

Из уравнений (4.2) и (5.2) выражаем

.

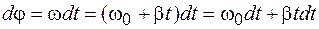Проинтегрируем полученное выражение:

.

Полагая, что в начальный момент времени 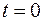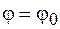, находим 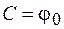. Тогда выражение для угла поворота принимает вид

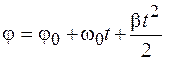. (5.3)

Если же твердое тело движется поступательно со скоростью 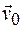и одновременно вращается с угловой скоростью 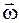, то линейная скорость движения любой его точки

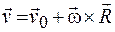. (5.4)

Таким образом, для описания поступательного движения тела вводятся величины: перемещение 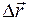, скорость v, ускорение a. Во вращательном движении аналогичными величинами являются угол поворота Δj, угловая скорость w, угловое ускорение b. Аналогия величин проявляется и в аналогии кинематических уравнений. Сравним уравнения, описывающие поступательное и вращательное движения тел с постоянными значениями линейного а и углового b ускорений (табл. 1).

Таблица 1