Вращательное движение твердого тела

Твердое тело — это система материальных точек, расстояние между которыми остается неизменным при взаимодействии системы с другими телами. Движение твердого тела бывает поступательным и вращательным. Всякое движение твердого тела можно представить как сумму движения названных двух типов. Покажем это для случая плоского движения, т. е. такого, при котором все точки тела перемещаются в параллельных плоскостях. В качестве примера плоского движения возьмем качение цилиндра по плоскости (рис.).

Качение цилиндра по плоскости. Стрелками обозначены линейные скорости различных точек цилиндра.

Скорость каждой точки цилиндра может быть представлена в виде:

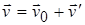(1.81)

где v₀ — скорость поступательного движения, одинаковая для всех точек тела, а v' линейная скорость точки, обусловленная вращением тела и разная для разных точек тела. Линейная скорость точки с радиусом-вектором r:

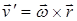. (1.82)

Таким образом, скорость точки при сложном движении тела имеет вид:

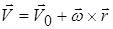. (1.83)

Отсюда следует, что существуют точки, суммарная скорость которых равна нулю относительно неподвижной системы отсчета (рис. 46).

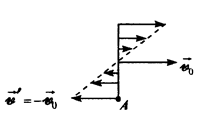
Скорость точки А цилиндра равна нулю относительно неподвижной системы отсчета

Геометрическое место точек, неподвижных в каждый рассматриваемый момент времени, образует прямую, которая является мгновенной осью вращения (рис.).

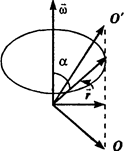
Проекции всех векторов r, лежащих на прямой 00', одинаковы. Прямая. 00' образует мгновенную ось вращения цилиндра.

В случае цилиндра, перемещающегося по плоскости, мгновенная ось совпадает с линией касания цилиндра плоскости. Видно, что мгновенная ось вращения не остается постоянной, а перемещается по мере движения тела. Скорости всех точек тела в каждый момент времени можно считать обусловленными вращением вокруг соответствующей мгновенной оси. Таким образом, плоское движение твердого тела можно рассматривать как ряд последовательных вращении вокруг мгновенных осей. В общем случае движение тела можно представлять как вращение вокруг мгновенной оси и одновременно поступательное движение вдоль этой же оси.