Кинетическая энергия твердого тела при вращении.

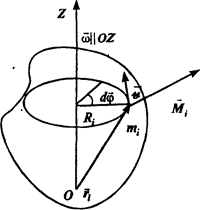Рассмотрим вращение тела вокруг неподвижной оси, которую назовем осью Z (рис.). Линейная скорость точки с массой m_i, равна v_i = ωR, где R, —расстояние точки до оси Z. Для кинетической энергии i-й материальной точки тела получаем выражение:

.

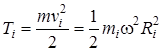Полная кинетическая энергия тела

.

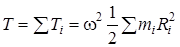Поскольку входящая сюда сумма представляет собой момент инерции относительно оси Z, получаем:

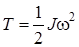(1.100)

Вычислим работу, совершаемую внешней силой при вращении твердого тела. Элемент работы .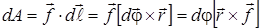

Последнее выражение есть момент внешней силы N , таким образом,

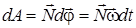. (1.101)

Полная работа может быть вычислена с помощью следующих формул:

. (1.202)

Приведем в заключение формулу, описывающую кинетическую энергию тела, совершающего плоское движение — поступательное, со скоростью V_c и вращение с частотой ω):

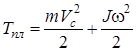(1.103)

Кинетическая энергия при плоском движении слагается из энергии поступательного движения со скоростью центра инерции тела и энергии вращения вокруг оси, проходящей через центр инерции.