Момент импульса. Момент силы
Мы видели, что механические свойства замкнутой системы не изменяются при ее параллельном переносе в пространстве. Это свойство является следствием однородности пространства, то есть отсутствием каких-либо выделенных точек пространства, физические свойства системы не должны изменяться также и при ее поворотах в пространстве, ввиду отсутствия в пространстве выделенных направлений, что означает изотропность пространства. Оказывается, что неизменность физических свойств системы при ее поворотах в пространстве также приводит к сохранению некоторой новой механической величины — момента импульса системы.
Рассмотрим систему, состоящую из двух взаимодействующих частиц, на которую действуют также внешние силы. Уравнения движения частиц имеют вид:
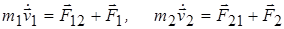 1.74
1.74
Умножим первое уравнение векторно слева на r1, а второе на r2.
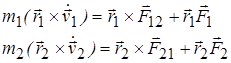 1.75
1.75
Поскольку 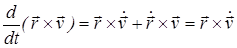 , т.к.
, т.к. 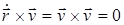 и F12 = ‑ F21,
и F12 = ‑ F21,
получим
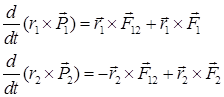 1.76.
1.76.
Сложим полученные уравнения:
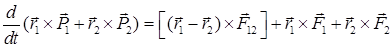 .
.
Векторы r1 - r2 и F12 коллениарны, поэтому
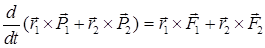 . 1.77.
. 1.77.
Если система замкнута 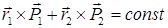 . Еще одна сохраняющаяся величина, которую называют моментом импульса.
. Еще одна сохраняющаяся величина, которую называют моментом импульса.
Примеры:
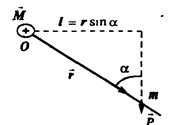

Момент импульса материальной точки, движущейся по прямой, относительно оси О
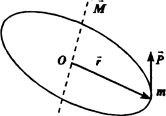
M = mvr
Момент импульса точки, движущейся по окружности
Моментом силы называют 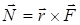 1.77
1.77
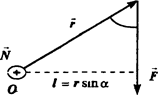
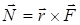 N = r·F·sinα = F·l 1.78.
N = r·F·sinα = F·l 1.78.
Момент силы. относительно точки О

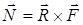 ; N = R·F·sinα. 1.79
; N = R·F·sinα. 1.79
Пара сил.
Продифференцируем 1.74 по времени:
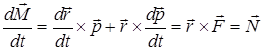 1.80
1.80
| Поступательное движение | Вращательное движение | Поступательное движение | Вращательное движение |
| Основной закон динамики | Работа и мощность | ||
| F∙Δt = mv2 ‑ mv1 | M∙Δt = J∙ω2 ‑ J∙ω1 | A=F∙s | A=М∙φ |
| F = m∙a | M = J∙ε | N = F∙v | N = M∙ω |
| Закон сохранения | Кинетическая энергия | ||
| момента импульса | импульса | ||
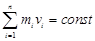
| 
| 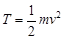
| 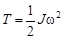
|
Дата добавления: 2015-08-08; просмотров: 776;
