Скорость и ускорение при криволинейном движении
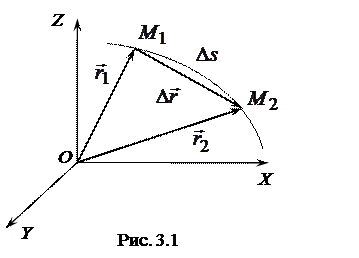 Рассмотрим движение материальной точки М в системе координат ХYZ по произвольной криволинейной траектории (рис. 3.1).
Рассмотрим движение материальной точки М в системе координат ХYZ по произвольной криволинейной траектории (рис. 3.1).
Пусть за время Dt материальная точка переместится из положения 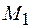 в положение
в положение 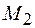 . При этом радиус-вектор изменится от
. При этом радиус-вектор изменится от 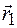 до
до 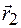 . Вектор
. Вектор 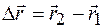 называется перемещением материальной точки.
называется перемещением материальной точки.
Средней скоростью движения за время Dt точки называют величину
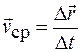 . (3.1)
. (3.1)
При неограниченном уменьшении промежутка времени Dt средняя скорость стремится к предельному значению, которое называется мгновенной скоростью:
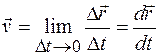 . (3.2)
. (3.2)
Мгновенная скорость равна производной перемещения по времени.
Длина 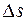 , отсчитанная по траектории, есть путь, пройденный точкой за время Dt. В отличие от перемещения путь - скалярная величина. В процессе движения его значение увеличивается, независимо от направления вектора скорости.
, отсчитанная по траектории, есть путь, пройденный точкой за время Dt. В отличие от перемещения путь - скалярная величина. В процессе движения его значение увеличивается, независимо от направления вектора скорости.
Направление вектора мгновенной скорости в любой точке траектории совпадает с направлением касательной к ней в этой точке.
Из формул (3.1), (3.2) следует, что единица скорости - метр на секунду (м/с).
Если вектор скорости изменяется в процессе движения, то важно знать, как быстро меняется скорость с течением времени. Ускорением 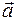 называют физическую величину, характеризующую быстроту изменения скорости как по модулю, так и по направлению.
называют физическую величину, характеризующую быстроту изменения скорости как по модулю, так и по направлению.
Если за время Dt скорость материальной точки изменилась от 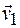 до
до 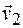 , т. е. на
, т. е. на 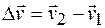 , то среднее ускорение определится выражением
, то среднее ускорение определится выражением
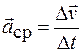 . (3.3)
. (3.3)
Переходя к пределу этого выражения при Δt ® 0, получим выражение для мгновенного ускорения
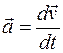 . (3.4)
. (3.4)
Единица ускорения - метр на секунду в квадрате (м/с2).
Ускорение численно равно изменению скорости за одну секунду.
В общем случае происходит изменение скорости по модулю и по направлению. В соответствии с этим вводятся две составляющие вектора ускорения: тангенциальное 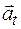 и нормальное
и нормальное 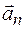 .
.
Тангенциальное ускорение направлено по касательной к траектории. Его числовое значение (модуль) определяется выражением 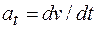 .
.
Нормальное ускорение направлено перпендикулярно вектору скорости (т. е. по нормали) и его модуль определяется выражением 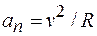 , где R - радиус дуги окружности, совпадающей с участком траектории, по которому движется материальная точка. Вектор
, где R - радиус дуги окружности, совпадающей с участком траектории, по которому движется материальная точка. Вектор 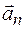 направлен по радиусу к центру окружности, отсюда другое его название - центростремительное ускорение.
направлен по радиусу к центру окружности, отсюда другое его название - центростремительное ускорение.
Из сказанного следует, что 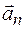 ^
^ 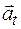 и полное ускорение движущейся точки
и полное ускорение движущейся точки
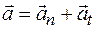 , (3.5)
, (3.5)
или по модулю
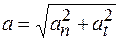 . (3.6)
. (3.6)
Воспользуемся формулами (3.2), (3.4) для получения так называемых кинематических уравнений, определяющих зависимость мгновенной скорости и координат от времени при равноускоренном движении ( 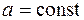 ).
).
Из уравнения (3.4) получим
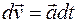 .
.
Для проекции вектора 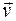 на ось ОХ находим
на ось ОХ находим
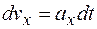 ,
,
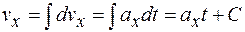 .
.
Значение постоянной интегрирования С находим из начальных условий: в момент времени 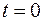 скорость движения
скорость движения 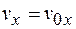 .
.
Получаем 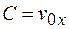 , и поэтому
, и поэтому
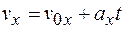 . (3.7)
. (3.7)
Из уравнения (3.2) выразим перемещение точки за время dt:
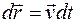 ,
,
и его проекцию
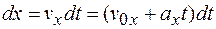 .
.
Для нахождения координаты х точки в момент времени t проинтегрируем полученное выражение:
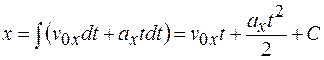 .
.
Постоянную интегрирования С найдем из начальных условий: при 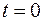
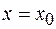 . С учетом этого получаем
. С учетом этого получаем 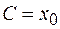 , и тогда
, и тогда
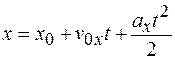 . (3.8)
. (3.8)
Аналогично записываются уравнения для координат y и z:
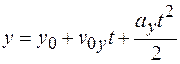 ,
,
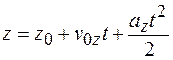 .
.
Дата добавления: 2015-08-08; просмотров: 1301;
