Траектория. Вектор перемещения. Скорость. Ускорение. Нормальное и тангенциальное ускорения
При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется тремя скалярными уравнениями:
х = х (t), y= y(t), z= z(t). (1.1)
эквивалентными векторному уравнению
r= r(t). (1.2)
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Если материальная точка движется в пространстве, то, как уже было сказано, она обладает тремя степенями свободы (координаты х, у и z), если по некоторой поверхности, то двумя степенями свободы, если по кривой, то одной степенью свободы.
Исключая t в уравнениях (1.1) и (1.2), получим уравнение траектории материальной точки.Траектория материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может бытьпрямолинейным или криволинейным.
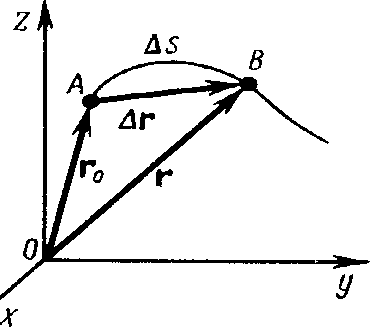 Рис.2
Рис.2
|
Рассмотрим движение материальной точки вдоль произвольной траектории (рис. 2). Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути  S и является скалярной функцией времени: S и является скалярной функцией времени: 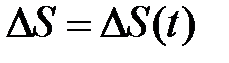 . .
|
Вектор 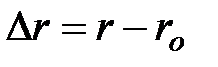 , проведенный из начального положения движущейся точки в положение ее в данный момент времени, называется вектором перемещения.
, проведенный из начального положения движущейся точки в положение ее в данный момент времени, называется вектором перемещения.
Для характеристики движения материальной точки вводится векторная величина - скорость, которая определяет как быстроту движения, так и его направление в данный момент времени.
Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени  ей соответствует радиус-вектор
ей соответствует радиус-вектор 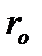 (рис.3).
(рис.3).
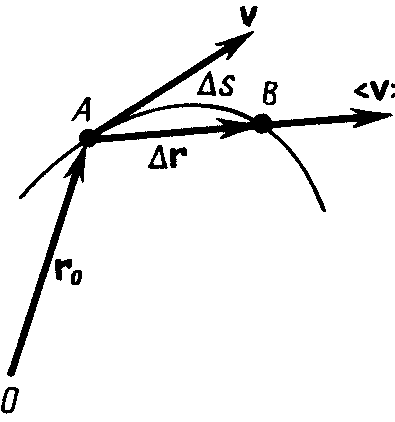 Рис.3
Рис.3
| В течение небольшого промежутка времени 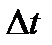 точка пройдет путь точка пройдет путь 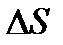 и получит элементарное перемещение и получит элементарное перемещение 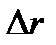 . Величина . Величина
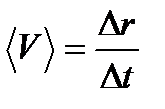 (1.3)
называется средней скоростью движения за время (1.3)
называется средней скоростью движения за время 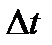 . Направление средней скорости совпадает с направлением . Направление средней скорости совпадает с направлением 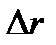 . Если в (1.3) перейти к пределу при . Если в (1.3) перейти к пределу при  , то получим выражение для мгновенной скорости v:
. , то получим выражение для мгновенной скорости v:
. 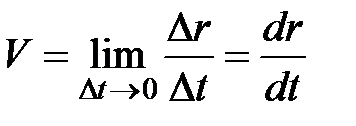 (1.4) (1.4)
|
Мгновенная скорость 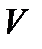 , таким образом, есть векторная величина, равная первой производной радиус-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис.3). По мере уменьшения
, таким образом, есть векторная величина, равная первой производной радиус-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис.3). По мере уменьшения 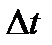 путь
путь 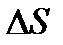 все больше будет приближаться к
все больше будет приближаться к 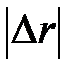 .
.
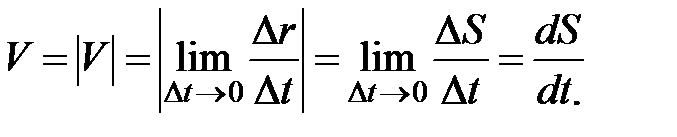 (1.5)
(1.5)
Таким образом, числовое значение мгновенной скорости равно первой производной пути по времени:
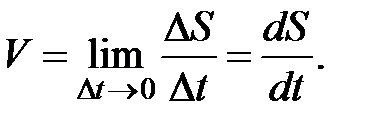 (1.6)
(1.6)
В случае неравномерного движения, когда числовое значение мгновенной скорости с течением времени изменяется, пользуются скалярной величиной 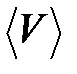 - средней скоростью неравномерного движения на данном участке:
- средней скоростью неравномерного движения на данном участке:

Из рис.3 вытекает, что 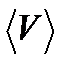 >
> 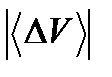 , так как
, так как 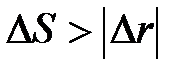 и только в случае прямолинейного движения
и только в случае прямолинейного движения 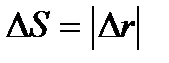 .
.
Если выражение 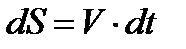 проинтегрировать по времени в пределах от
проинтегрировать по времени в пределах от  до
до 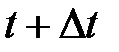 , то найдем длину пути, пройденного точкой за время
, то найдем длину пути, пройденного точкой за время  :
:
 (1.7)
(1.7)
В случае равномерного движения, когда числовое значение мгновенной скорости постоянно, выражение (1.7) примет вид
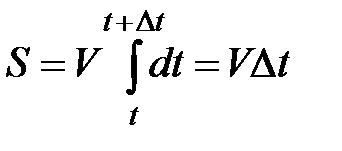
Путь, пройденный точкой за промежуток времени от 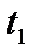 до
до 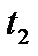 , определяется интегралом
, определяется интегралом
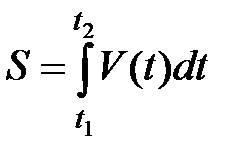 (1.8)
(1.8)
Дата добавления: 2015-08-11; просмотров: 3962;
