Вектор в пространстве
В пространстве вектор силы проецируется на три взаимно перпендикулярные оси координат. Проекции вектора образуют ребра прямоугольного параллелепипеда, вектор силы совпадает с диагональю (рис. 1.32).Модуль вектора может быть получен из зависимости
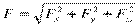
где Fx = F cos αx;
Fн = F cos αy;
Fя = F cos αz
αx, ay, az, — углы между вектором F и осями координат. Рис. 1.32
Пространственная сходящаяся система сил
Пространственная сходящаяся система сил — система сил, не лежащих в одной плоскости, линии действия которых пересекаются в одной точке.
Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник (рис. 1.32),
FΣ = F1 + F2 + F3 + … + Fn.
Доказано, что равнодействующая системы сходящихся сил приложена в точке пересечения линий действия сил системы.
Модуль равнодействующей пространственной системы сходящихся сил можно определить аналитически, использовав метод проекций.
Совмещаем начало координат с точкой пересечения линий действия сил системы. Проецируем все силы на оси координат и суммируем соответствующие проекции (рис. 1.33).
Получим проекции равнодействующей на оси координат:
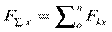 ;
; 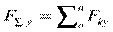 ;
; 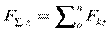 .
.
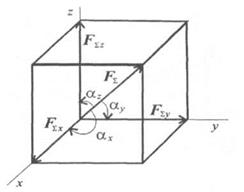
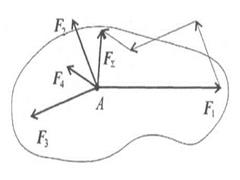
Рис. 1.33 Рис.1.34
Модуль равнодействующей системы сходящихся сил определим по формуле
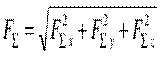 .
.
Направление вектора равнодействующей определяется углами
ax = (FΣ ^ F Σx); αy = (FΣ ^ F Σy); αz = (FΣ ^ F Σz),
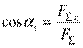
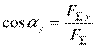
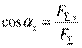
где
Дата добавления: 2015-08-08; просмотров: 1096;
