Приведение произвольной пространственной системы сил к центру О
Дана пространственная система сил (рис. 7.5а). Приведем ее к центру О.
Силы необходимо параллельно перемещать, при этом образуется система пар сил. Момент каждой из этих пар равен произведению модуля силы на расстояние до центра приведения.
В центре приведения возникает пучок сил, который может быть заменен суммарной силой (главный вектор) Fгл (рис. 7.56).
Моменты пар сил можно сложить, получив суммарный момент системы Мгл (главный момент).
Таким образом, произвольная пространственная система сил приводится к главному вектору и главному моменту.
Главный вектор принято раскладывать на три составляющие, направленные вдоль осей координат (рис. 7.5в).
Обычно суммарный момент раскладывают на составляющие: три момента относительно осей координат.
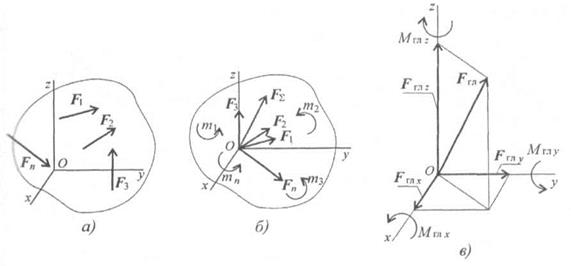
рис.
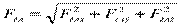 Абсолютное значение главного вектора (рис. 7.56) равно
Абсолютное значение главного вектора (рис. 7.56) равно
где 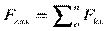 ;
; 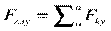 ;
; 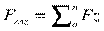
Абсолютное значение главного момента определяется по формуле 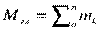 .
.
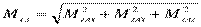 ,
,
где 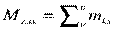 ;
; 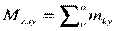 ;
; 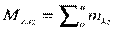 .
.
Дата добавления: 2015-08-08; просмотров: 866;
