Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
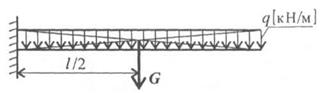 Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
Взадачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 1.26).
Рис. 1.26
где q — интенсивность нагрузки; / — длина стержня;
G = ql — равнодействующая распределенной нагрузки.
Применяют следующие виды опор.
Жесткая заделка (защемление) (рис. 6.2)
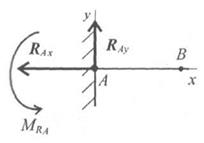 Опора не допускает перемещений и поворотов. Неизвестными в данном случае являются не только значение и направление реакции, но и точка ее приложения. Заделку заменяют двумя составляющими силы RAx и RAy и парой с моментом MR.
Опора не допускает перемещений и поворотов. Неизвестными в данном случае являются не только значение и направление реакции, но и точка ее приложения. Заделку заменяют двумя составляющими силы RAx и RAy и парой с моментом MR.
Для определения этих неизвестных удобно использовать систему уравнений в виде
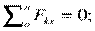
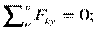
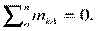
Каждое уравнение имеет одну неизвестную величину и решается без подстановок.
Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например В: рис.1.27
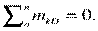
Шарнирно-подвижная опора (рис. 1.28) Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. В этой опоре известны точки приложения опорной реакции – центр 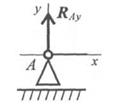 шарнира и ее направление – перпендикуляр к опорной плоскости. Здесь остается неизвестным значение опорной реакции
шарнира и ее направление – перпендикуляр к опорной плоскости. Здесь остается неизвестным значение опорной реакции 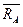 Реакция
Реакция 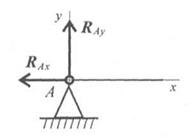 направлена перпендикулярно опорной поверхности.
направлена перпендикулярно опорной поверхности.
Рис. 1.28
Шарнирно-неподвижная опора (рис. 1.29) Опора допускает поворот вокруг шарнира, но не допускает никаких линейных перемещений. В данном случае известна только точки приложения опорной реакции – центр шарнира; направление и значение опорной реакции неизвестны и может быть заменена двумя составляющими силы вдоль осей координат. Обычно вместо определения значения Рис.1.29
 и направления (полной) реакции
и направления (полной) реакции 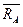 находят ее составляющие
находят ее составляющие 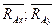
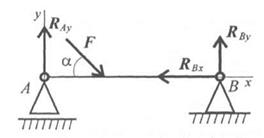
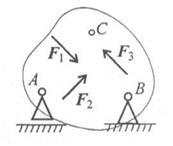 Балка на двух шарнирных опорах (рис.1.30). Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй формуле:
Балка на двух шарнирных опорах (рис.1.30). Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй формуле:
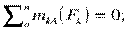
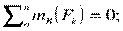
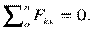
рис.1.30
Составляются уравнения моментов относительно точек крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила. Из уравнения  определяется реакция RBx.
определяется реакция RBx.
Из уравнения 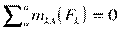 определяется реакция RBy.
определяется реакция RBy.
Из уравнения 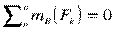 определяется реакция RAy.
определяется реакция RAy.
Для контроля правильности решения используется дополнительное уравнение
 рис.1.31
рис.1.31
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 1.31):
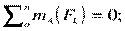
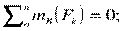
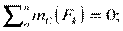
|
Дата добавления: 2015-08-08; просмотров: 1366;
