Теорема о моменте равнодействующей (теорема Вариньона)

В общем случае произвольная плоская система сил приводится к главному вектору F'_гл и к главному моменту М_гл относительно выбранного центра приведения, причем главный момент равен алгебраической сумме моментов заданных сил относительно точки О:

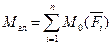
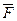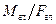Было показано, что можно выбрать центр приведения (рис. 1.25, точка С), относительно которого главный момент системы равен нулю, и система сил приведется к одной равнодействующей, равной по модулю главному вектору. Определим момент равнодействующей относительно точки О. Учитывая, что плечо ОС силы равно , получаем

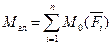
Полученное уравнение выражает теорему Вариньона: момент равнодействующей плоской системы сил относительно произ­вольно взятой точки равен алгебраической сумме моментов со­ставляющих сил относительно той же точки.

Из теоремы Вариньона следует, что главный момент плоской системы сил относительно любой точки, лежащей на линии дей­ствия ее равнодействующей, равен нулю. Рассмотрим применение теоремы Вариньона на конкретных примерах.