Приведение силы к точке.

Произвольная плоская система сил представляет собой систему сил, линии действия которых расположены в плоскости каким угодно образом (рис. 1.23).

Возьмем силу 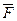, приложенную в точке С. Требуется пере­нести эту силу параллельно самой себе в некоторую точку О.

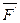Приложим в точке О две силы и 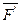, противоположно направленные, равные по значению и параллельные заданной силе 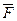,т. е. F' = F" = F. От приложения в точке О этих сил состояние тела не изменяется, так как они взаимно уравновешиваются. Полученную систему трех сил можно рассматривать как состоящую из силы 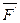, приложенной в точке О, и пары сил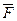 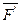с моментом М = Fa. Эту пару сил называют присоединенной, а ее плечо а равно плечу силы 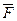относительно точки О (рис. 1.23, а).

Таким образом, при приведении силы 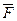к точке, не лежащей на линии действия силы, получается эквивалентная система, состоящая из силы, такой же по модулю и направлению, как и сила 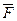, и присоединенной па­ры сил, момент которой равен моменту данной силы относи­тельно точки приведения (Теорема Пуансо):

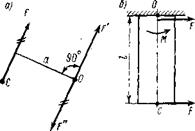
М₀ ( 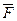) = Fa. Рис.1.23