Приведение к управляемой канонической форме.
Вернемся к рассмотрению вопроса о выборе матрицы преобразования Т, которая преобразует уравнения состояния с матрицами А и В к канонической форме с матрицами 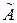 и
и  .
.
Показано, что матрицы управляемости 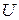 и
и 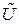 систем, описываемых уравнениями в обычной и канонической управляемой форме, связаны соотношением
систем, описываемых уравнениями в обычной и канонической управляемой форме, связаны соотношением 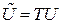 . Отсюда, искомая матрица преобразования для системы с одним входом
. Отсюда, искомая матрица преобразования для системы с одним входом
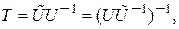 (*)
(*)
где обратная матрица управляемости 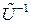 может быть представлена в виде
может быть представлена в виде
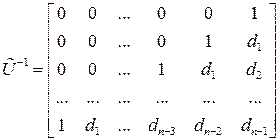 . (**)
. (**)
Здесь  ,
, 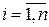 , являются коэффициентами характеристического многочлена матрицы А:
, являются коэффициентами характеристического многочлена матрицы А:
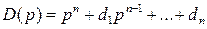 .
.
Как видим, матрица подобия Т, преобразующая систему к канонической управляемой форме, существует лишь тогда, когда матрица управляемости U невырожденная, то есть  . Другими словами, когда система является полностью управляемой.
. Другими словами, когда система является полностью управляемой.
Дата добавления: 2015-08-14; просмотров: 2369;
