Общий случай для управляемой канонической формы

Рассмотрим решение задачи размещения полюсов для случая, когда объект описывается уравнением состояния в управляемой канонической форме

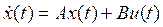, (12)

где

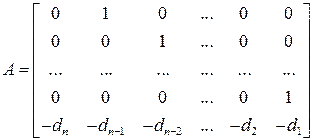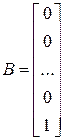, . (13)

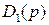Последняя строка матрицы включает в себя коэффициенты d_i характеристического многочлена объекта управления , взятые с отрицательным знаком.

В соответствии с (6) уравнение состояния проектируемой системы

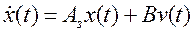, (6)

где согласно (7)

,

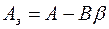причем - n-мерный вектор-строка представляет собой векторный коэффициент обратной связи по состоянию x(t).

Выберем вектор 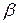так, чтобы проектируемая система имела заданное размещение полюсов, определяемое характеристическим многочленом желаемой системы

.

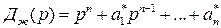Для этого найдем

. (14)

Подставляя в 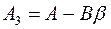(7) выражения (13) и (14) для и , получаем

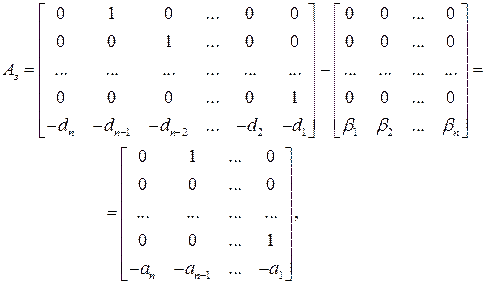(15)

где

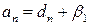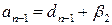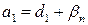; ;…; . (16)

Поскольку проектируемая система описывается уравнением состояния (6), в котором матрицы 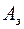и 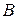согласно (15) и (13)соответствуют управляемой канонической форме, то элементы последней строки матрицы 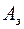представляют собой коэффициенты 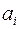характеристического многочлена проектируемой системы

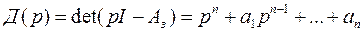, (17)

взятые с обратным знаком.

Полагая в (16) 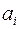равными желаемым значениям 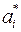, получаем значения элементов

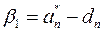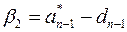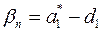, ,…, , (18)

вектора 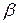, обеспечивающие желаемое расположение полюсов проектируемой системы.