Формула Аккермана
Если исходное уравнение состояния объекта отличается от управляемой канонической формы, то в случае управляемости объекта для определения вектора обратной связи по состоянию используют следующую трехэтапную процедуру.
1. Преобразуют исходную модель объекта в управляемую каноническую форму, используя матрицу преобразования
. (*)
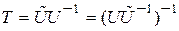2. Находят вектор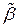 
обратной связи по преобразованному состоянию 
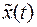, применяя (18).
3. Преобразуют вектор 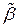в вектор обратной связи по исходному состоянию 
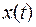. используя
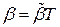. (19)
Формула Аккермана объединяет эти шаги в одну формулу
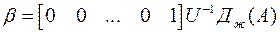, (20)
где матричный многочлен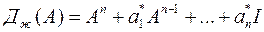 
составлен с помощью коэффициентов характеристического уравнения желаемой системы.
Пример. Пусть объект описывается уравнением состояния
,
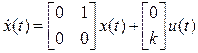а желаемый характеристический многочлен имеет вид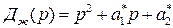 
.
Так как
,
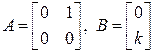то передаточная функция объекта имеет вид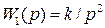 
, т.е. объект представляет собой двойной интегратор. Отсюда, 
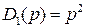. Следовательно, n=2, 
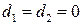иматрица управляемости
.
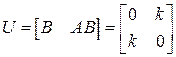В соответствии с ( ** )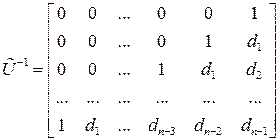 
обратная матрица
.
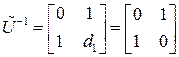Легко показать, что
, 
,
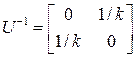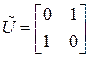так что согласно (*)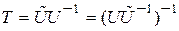
.
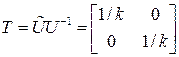Используя (18)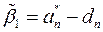 
, 
,…, 
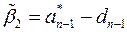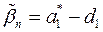, находим
, 
.
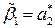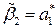Согласно (19)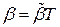
,
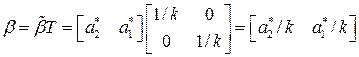что совпадает с выражением, полученным ранее другим путем.
Команда MATLAB: acker (A,B, Рр).
Пример. Пусть в условиях предыдущего примера коэффициенты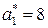 
, 
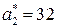, так что полюсы желаемой системы 
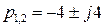, k = 1. Тогда применяя команду
l = acker(A,B, [-4+j*4 -4-j*4]),
можно найти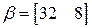 
.
Сделаем несколько замечаний, касающихся рассмотренного метода размещения полюсов.
1. Матрица T может быть найдена только в том случае, когда существует обратная матрица управляемости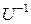 
. Следовательно, любое расположение полюсов проектируемой системы с помощью обратной связи по состоянию можно обеспечить, если объект управления полностью управляем, т.е. если матрица управляемости объекта 
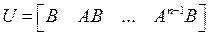является невырожденной, так что 
.
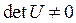2. Спроектированная в соответствии с формулами (7), (18) и (19) система не удовлетворяет условию астатизма, т.е. ее передаточная функция
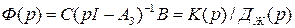
не равна единице при p=0, другими словами, спроектированная система является статической. Здесь K(p) числитель ПФ объекта.
Если выбрать закон управления в виде
,
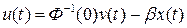то передаточная функция проектируемой системы
.
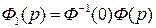Так как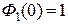 
, то, как видим, введение наряду с обратной связью по состоянию прямой связи по задающему воздействию
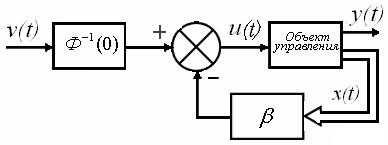
Рис.3
(рис. 3) обеспечивает астатизм проектируемой системы.
Дата добавления: 2015-08-14; просмотров: 2480;