Замечание. Наблюдатели нужны только для реализации обратной связи по состоянию.

Если известна математическая модель объекта

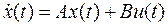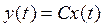, , (1)

то для того, чтобы это можно было сделать, как мы покажем позднее, объект должен быть полностью наблюдаем. Рассмотрим ряд способов построения наблюдателей.

Наблюдатели полного порядка. Наблюдатели, позволяющие по результатам измерения входа 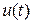и выхода 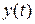объекта, описываемого уравнением ( 1 ), восстановить все 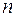переменных состояния 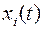, , 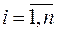называют наблюдателями полного порядка . Они должны строиться так, чтобы разница между оценкой состояния 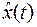и действительным состоянием 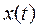была бы как можно меньше. Оценка состояния 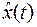должна со временем сходиться к истинному состоянию 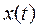, т.е.

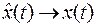при .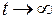

Идея одного из методов построения такого наблюдателя заключается в следующем.

Если нельзя непосредственно измерить состояние объекта управления, то, создав устройство, описываемое тем же уравнением состояния

,

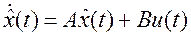что и сам объект, и подав на его вход сигнал управления 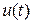, на выходе можно получить вектор 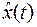, изменяющийся по такому же закону, что и вектор состояния 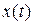. Однако реакция объекта, а следовательно, изменение вектора состояния в соответствии с уравнением (1), зависит не только от сигнала 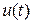, но и от начального состояния 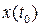, т.е. от действительного состояния объекта в тот момент, когда началось восстановление. Если бы это значение 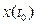было известно, то его можно было ввести в рассматриваемый наблюдатель, и тогда выходная величина наблюдателя изменялась по такому же закону, что и состояние объекта. К сожалению, действительное состояние объекта является, по условиям задачи, неизвестным и неизмеримым для любого момента времени 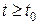. При этом, на первый взгляд, кажется невозможным по описываемому методу построить наблюдатель, обеспечивающий требуемую точность вычисления 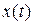при произвольных начальных состояниях объекта. К счастью это не так. Действительно, если поведение наблюдателя корректировать за счет введения сигнала, пропорционального разности между выходным сигналом объекта 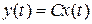и прогнозируемым его значением

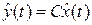(2)

то можно создать условия для автоматического устремления оценки 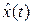к 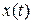независимо от величины начального отклонения .

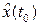Структурная схема наблюдателя, построенного в соответствии с приведенными рассуждениями для объекта с одним входом и одним выходом (l=r=1), представлена на рис. 4.

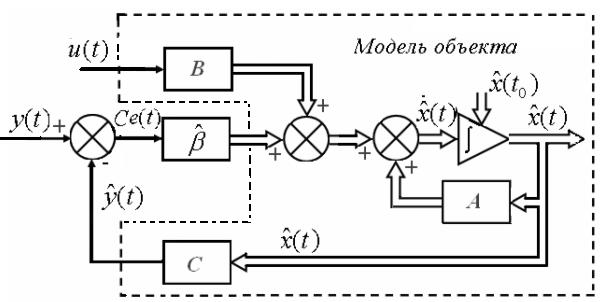
Рис. 4

Если начальные состояния объекта 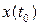и наблюдателя 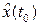не будут одинаковыми (обычно 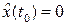), то реакция наблюдателя 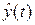также будет отличаться от выхода объекта 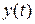. При этом разность 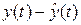с векторным коэффициентом 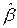подводится к входу интегратора и корректирует начальное значение оценки 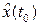. Очевидно, что 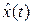будет изменяться до тех пор, пока значение 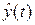не станет равным выходу объекта 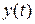, другими словами, пока не будет выполняться равенство 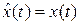. Естественно, если наблюдатель представляет собой устойчивое устройство.

Как видно из рис. 4, уравнение наблюдателя имеет вид

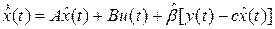. (3)

Здесь через 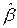обозначен векторный коэффициент (l-вектор), называемый параметром наблюдателя. Введем в рассмотрение ошибку оценивания

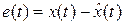. (4)

Вычитая (3) из 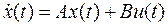( 1 ), с учетом 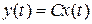и ( 4 ) получаем

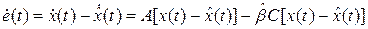(5)

или

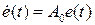, (6)

где матрица

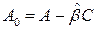(7)

называется матрицей наблюдателя.

Единственным параметром наблюдателя является векторный коэффициент 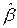, поэтому проектирование наблюдателя по существу сводится к подбору элементов этого вектора. При этом руководствуются следующими соображениями.

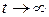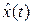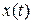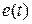1. Из (6) следует, что при оценка будет стремиться к , а будет стремиться к нулю только в том случае, если наблюдатель является устойчивым, т.е. если все корни 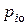, , 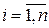характеристического уравнения наблюдателя

,

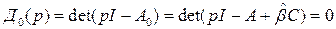называемые также полюсами наблюдателя, имеют отрицательную вещественную часть, т.е. будут левыми. Кстати, полюсы являются также собственными значениями матрицы наблюдателя 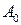. Таким образом, параметр 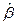выбирается, прежде всего, из условия устойчивости наблюдателя.

2. Но одной устойчивости недостаточно. Надо еще обеспечить хорошее быстродействие наблюдателя, т.е. надо выбрать 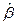так, чтобы обеспечить быструю сходимость 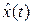к 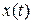. Исходя из этого требования, подбором 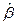надо добиться не только того, чтобы полюсы наблюдателя были левыми, но и находились на достаточно большом расстоянии от мнимой оси.

3. Однако чем больше быстродействие наблюдателя, тем меньше его помехоустойчивость по отношению к шуму измерения 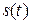выходного сигнала. При построении наблюдателя мы полагали, что выход объекта измеряется точно. Фактически моделью наблюдаемого на выходе датчика сигнала 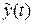является сумма выхода 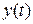и высокочастотного шума измерения 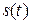, так что 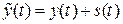. Поэтому желательно, чтобы наблюдатель обладал хорошими фильтрующими свойствами, т.е. обладал достаточно большой инерционностью. Только при этом условии шум измерения будет оказывать малое влияние на точность оценивания вектора состояния. Следовательно, подбором 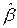надо добиться, чтобы полюсы наблюдателя были не слишком удалены от мнимой оси.

Как видим, условия большого быстродействия и высокой помехоустойчивости являются противоречивыми, поэтому при выборе 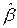необходимо находить компромиссное решение.