Замкнутые системы с наблюдателями (Системы управления, основанные на модели).

Предположим, что ОУ с одним входом и одним выходом (l=r=1), описываемый уравнениями

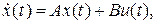(1)

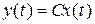, (2)

полностью управляем и наблюдаем.

Пусть для этого ОУ мы нашли такое управление (такой закон управления с обратной связью по состоянию)

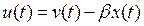, (3)

где 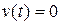- задающее воздействие, а 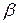- векторный коэффициент ОС по состоянию, при котором полюса 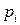, другими словами, корни характеристического уравнения замкнутой системы с обратной связью по состоянию

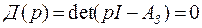
имеют фиксированное расположение 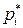, удовлетворяющее требованиям, предъявляемым к проектированной системе, то есть мы нашли такой вектор 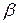, который обеспечивает равенство многочленов проектируемой и желаемой систем, .

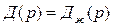Но вектор 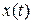неизмерим!

В этом случае кажется разумным использовать другой закон управления, а именно закон с обратной связью по выходу (по оценке состояния), получаемый из (3) 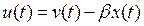путем замены 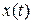на оценку вектора состояния :

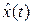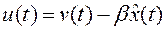, (4)

где оценка состояния определяется с помощью наблюдателя, описываемого уравнением

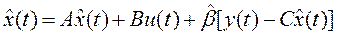. (5)

Здесь 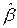- векторный параметр наблюдения.

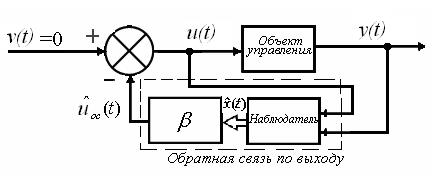
Закон управления, определяемый уравнениями (4)и (5), совместно с уравнениями объекта (1) и (2) формирует замкнутую систему с наблюдателем (систему управления, основанную на модели). Последнее название связано с тем обстоятельством, что наблюдатель включает в себя модель объекта управления.

Упрощенная операционная структурная схема такой системы представлена на рисунке ниже.

Однако естественно возникают вопросы. Как замена в законе управления (3) 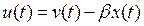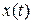на 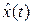повлияет на свойства системы? Каково расположение полюсов замкнутой системы с наблюдателем?

Для ответа на эти вопросы нужно найти уравнение состояния полученной замкнутой системы с наблюдателем. С этой целью подставим 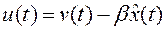(4) в уравнение состояния объекта 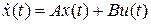(1). При этом находим

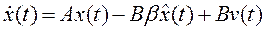. (6)