Реализация замкнутой системы с наблюдателем
Замкнутую систему с наблюдателем можно реализовать с помощью динамической обратной связи по выходу в рамках классической теории управления. С этой целью, полагая 
 , из (4)
, из (4) 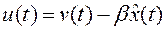 получаем выражение для управления в виде
получаем выражение для управления в виде
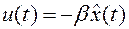 . (10)
. (10)
Подставляя (10) в (5) 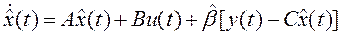 , находим
, находим
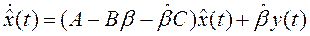 . (11)
. (11)
В изображениях по Лапласу уравнения (10) и (11) выглядят так,
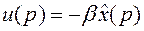 , (12)
, (12)
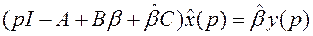 . (13)
. (13)
Выражая 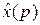 из (13) и подставляя полученный результат в (12), находим
из (13) и подставляя полученный результат в (12), находим
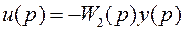 ,
,
где
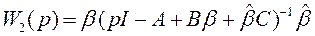 (14)
(14)
является ПФ обратной связи по выходу. Учитывая, что преобразования Лапласа выхода 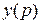 и входа
и входа 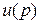 объекта связаны между собой
объекта связаны между собой
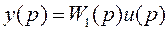
посредством ПФ ОУ
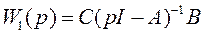 ,
,
можно построить динамическую структурную схему замкнутой системы с наблюдателем (рис. ниже) как объект управления, охваченный отрицательной обратной связью с ПФ 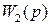 .
.
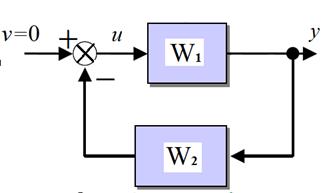
Пример. Пусть в качестве ОУ используется двойной интегратор, для которого
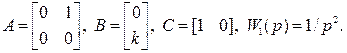
Желаемые значения полюсов и коэффициентов характеристического уравнения проектируемой системы имеют вид 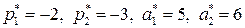 , Отсюда желаемые значения коэффициентов обратной связи по состоянию в соответствии с ранее полученными формулами
, Отсюда желаемые значения коэффициентов обратной связи по состоянию в соответствии с ранее полученными формулами
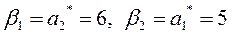 .
.
Предположим, что желаемые значения полюсов и коэффициентов характеристического уравнения наблюдателя
 . Отсюда желаемые значения элементов векторного параметра наблюдателя в соответствии с выражениями полученными ранее
. Отсюда желаемые значения элементов векторного параметра наблюдателя в соответствии с выражениями полученными ранее
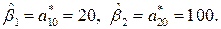
Подставляя численные значения 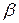 и
и 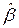 в (14), получаем
в (14), получаем 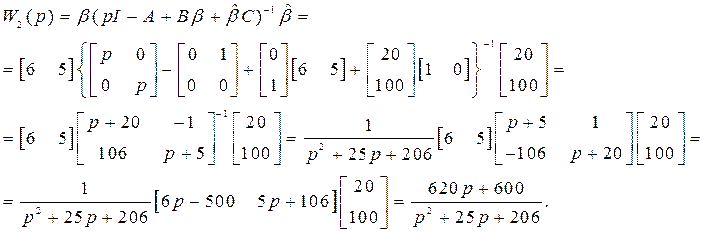 При этом ПФ замкнутой системы
При этом ПФ замкнутой системы
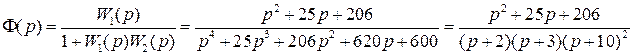 .
.
Дата добавления: 2015-08-14; просмотров: 790;
