Линейная квадратичная задача (ЛК-задача) оптимального управления

Проблема, возникающая при реализации рассмотренных выше методов выбора расположения полюсов заключается в том, что они (методы) полностью игнорируют допустимую величину управления. Поэтому проектировщику нужно осуществлять множество итераций, чтобы добиться желаемого результата. Задача остается прежней: как можно быстрее вернуть систему из возмущенного начального состояния в нулевое состояние при ограничении максимального значения управления.

Рассмотрим альтернативный метод расположения полюсов, получивший название линейной квадратичной (ЛК) задачи оптимального управления или задачи линейного квадратичного регулятора (ЛКР).

Пусть ОУ описывается уравнением состояния

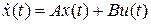, (1)

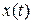есть n- вектор, 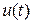есть r-вектор. Начальное состояние есть 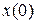. Мы предполагаем, что все переменные состояния измеримы и ставим задачу найти закон управления с обратной связью по состоянию (другими словами, найти коэффициент обратной связи по состоянию )

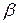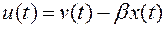, (2)

который обеспечивает желаемые свойства для проектируемой замкнутой системы, другими словами, желаемое расположение полюсов замкнутой системы. С учетом этого закона уравнение состояния замкнутой системы можно записать как

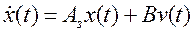, (3)

где 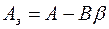является матрицей замкнутой системы и 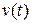задающее воздействие. Заметим, что матрица выхода C не используется в данном законе управления.

Условия, в которых биологическая жизнь может существовать, являются очень узкими. В ходе эволюции изменение температуры воздуха на несколько градусов приводило к исчезновению целых популяций. Источники энергии живого организма, такие как клетки, весьма ограничены по своей мощности. Поэтому многие биологические организмы развивались так, чтобы они постепенно становились оптимальными в смысле использования минимальных усилий, требуемых для поддержания своего гомеостазиса или равновесия. С очень малыми затратами на выделение соответствующих химических продуктов через мембрану клетки, клетка может поддерживать разность потенциалов вдоль мембраны, необходимую для ее (клетки) жизнедеятельности и нормального функционирования.

Так как многие встречающиеся в живой природе системы являются оптимальными, то разумно спроектировать искусственные (рукотворные) регуляторы так, чтобы они были оптимальными. Чтобы спроектировать оптимальную обратную связь по состоянию, мы, прежде всего, должны определить скалярный показатель качества (другое название, целевая функция, функция стоимости) в виде функционала

. (4)

Мы предполагаем, что задающее воздействие равно нулю, 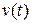=0, т.к. нас интересует здесь свойство внутренней устойчивости замкнутой системы, т.е. мы рассматриваем задачу регулирования. Подставляя (2) 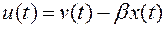при 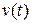=0 в (4), получаем

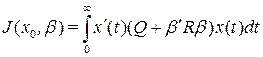. (5)

Цель оптимального проектирования состоит в том, чтобы найти такой коэффициент обратной связи по состоянию 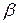, который минимизирует показатель качества J.