Астатические системы с обратной связью по состоянию

Метод размещения полюсов при нулевом задающем воздействии приводит к статической системе. Введение прямой связи по задающему воздействию позволяет добиться астатизма. Однако полученная система теряет астатические свойства при изменении параметров ОУ. Рассмотрим еще один метод проектирования астатической системы с обратной связью по состоянию, свободный от этого недостатка.

В соответствии с принципом внутренней модели для безошибочного воспроизведения в установившемся режиме постоянного задающего воздействия v(t)=v₀ = const замкнутая система с единичной обратной связью должна включать в себя хотя бы одно интегрирующее звено (один интегратор). Этот принцип можно осуществить и в рамках метода размещения полюсов.

Пусть ОУ с одним входом и одним выходом описывается уравнениями

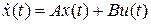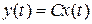, . (1)

Обозначим через v₀ = const желаемое установившееся значение для управляемой величины y.

Интегратор можно ввести в рассмотрение, используя новую скалярную переменную состояния

,

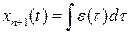являющуюся интегралом от ошибки управления

.

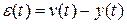Отсюда получаем скалярное дифференциальное уравнение

.

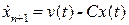Расширенный таким образом ОУ с двумя входами v(t) и u(t), и составным вектором состояния 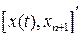описывается следующим уравнением состояния

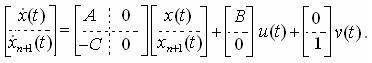
Для нового ОУ можно решить задачу размещения полюсов с помощью обратной связи по расширенному состоянию. При этом управление имеет вид

.

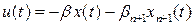Операционная структурная схема замкнутой системы с интегратором и обратной связью по состоянию представлена на рисунке.

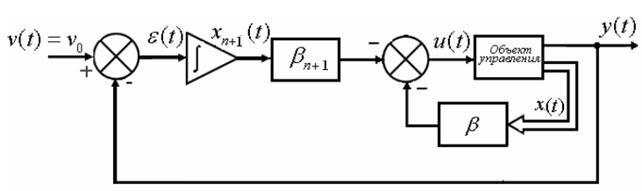
Если полюсы расширенной замкнутой системы являются левыми (система устойчивая), то 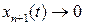при v(t)= const и тогда в установившемся состоянии 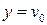. Разумеется, что обеспечить любое расположение полюсов замкнутой системы можно только тогда, когда расширенный объект полностью управляем.

Поскольку собственные значения матрицы 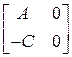являются непрерывной функцией ее элементов, то ошибка в установившемся состоянии будет нулевой, если замкнутая система устойчивая, даже при наличии малых погрешностей в модели объекта (малых ошибок моделирования), т.е. имеет место робастный астатизм.