Лекция 10. Введем в рассмотрение ошибку оценивания

Введем в рассмотрение ошибку оценивания

.

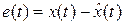Отсюда

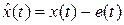
и, следовательно, уравнение (6) принимает вид

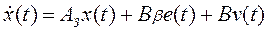, (7)

где 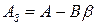- матрица замкнутой системы при использовании закона управления 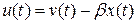. Как мы показали в параграфе, посвященном наблюдателю, уравнение для ошибки имеет вид

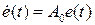, (8)

где 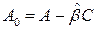является матрицей наблюдателя. Итак, состояние системы с наблюдателем описывается уравнениями (7) и (8). Введя в рассмотрение составной вектор 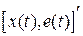размерностью 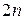, систему из этих уравнений можно представить в векторно-матричной форме

(9)

Следовательно, роль матрицы системы с наблюдателем играет блочная матрица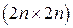

,

как видим, имеющая треугольный нижний блочный вид. Отсюда характеристический многочлен замкнутой системы с наблюдателем

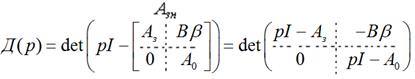
Здесь 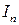- единичная матрица размерности 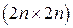, а 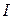- единичная матрица размерности .

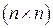В теории матриц показано, что определитель треугольной блочной матрицы равен произведению определителей матриц, расположенных на главной диагонали, поэтому

,

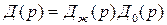где

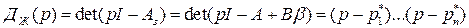
представляет собой характеристический многочлен желаемой системы, а

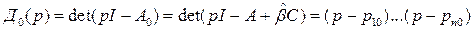
является характеристическим многочленом наблюдателя.

Следовательно, введение в систему наблюдателя не изменяет расположения найденных в соответствии с требованиями качества полюсов 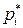, , 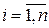проектируемой системы, а лишь добавляет полюсы наблюдателя .

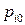Это свойство систем с наблюдателем позволяет разделить задачу проектирования системы на две независимые части, включающие в себя:

1. выбор векторного коэффициента 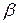обратной связи по состоянию, исходя из желаемого расположения полюсов 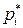, , 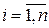проектируемой системы. Эта задача, которую мы решали для случая, когда вектор состояния измерим,

2. выбор векторного коэффициента 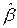наблюдателя в соответствии с теми требованиями, которые предъявляются к расположению полюсов 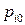, , 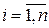наблюдателя. Полученный вывод носит название теоремы разделения.

Изменяя параметр 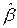, можно найти такие значения полюсов наблюдателя 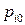, при которых свойства проектируемой системы мало будут отличаться от свойств желаемой системы. При этом рекомендуется выбирать полюсы наблюдатели из условия .

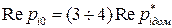Здесь 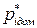- доминирующие полюсы желаемой системы.