Выбор расположения полюсов проектируемой системы

В предыдущих параграфах текущего раздела мы показали, каким путем можно выбрать коэффициент обратной связи по состоянию, если определено желаемое расположение полюсов замкнутой системы. Однако при этом возникает вопрос классической теории управления: как найти расположение полюсов, чтобы добиться желаемых свойств для проектируемой системы, другими словами, как выбрать желаемый характеристический многочлен замкнутой системы. 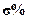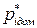Один из возможных путей решения этой проблемы: использовать временные показатели качества (t_р, t_н, ) для определения доминирующих полюсов желаемой системы – корней уравнения второго порядка

.

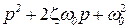Затем расположить остальные полюсы так, чтобы они были «намного быстрее», чем доминирующие полюсы. Как пример, можно их выбрать из условия 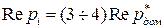, т.е., чтобы их вещественная часть была в 3-4 раза больше, чем вещественная часть доминирующих полюсов 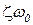. При этом надо осторожно относиться к смещению этих полюсов слишком далеко влево от мнимой оси, т.к. оно приведет к большому по величине управлению. Это первый путь.

Второй возможный путь выбрать полюсы замкнутой системы, так чтобы система реагировала на задающее воздействие аналогично некоторой желаемой системе, свойства которой близки к тем, что мы ожидаем от проектируемой системы. Другими словами, установить полюсы проектируемой системы равными полюсам желаемой системы (прототипа, прообраза). В качестве последней можно, например, выбрать систему k-го порядка с ПФ

,

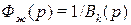где 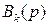многочлены Бесселя. Переходная характеристика системы 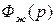для различных значений k и расположение корней нормированного многочлена Бесселя, соответствующих времени переходного процесса в 1с., представлены на рис. ниже.

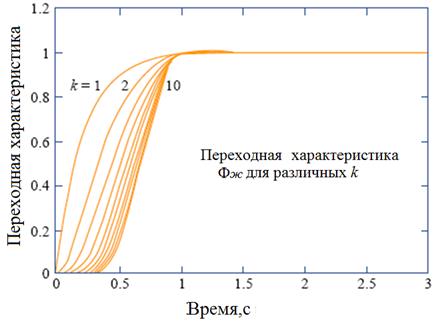
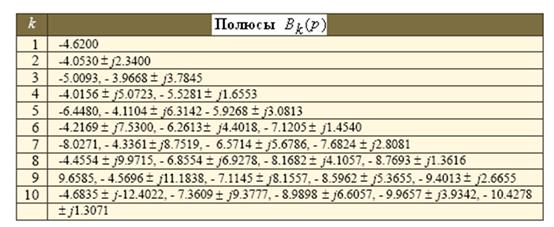
Все многочлены масштабированы так, чтобы длительность переходного процесса была равна 1с. Если поделить все полюсы на t_р, то можно изменить длительность переходного процесса до желаемого значения t_р.

Процедура проектирования для системы n-го порядка:

− Определить желаемое время переходного процесса t_р;

− Выбрать порядок многочлена k=n из таблицы;

− Разделить значения всех полюсов 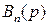на t_р;

− Сформировать желаемый характеристический многочлен 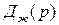и использовать процедуру acker/place;

− Осуществить симуляцию спроектированной системы с целью оценить ее качество и максимальную величину управления.

Пример. Пусть объект управления описывается уравнением состояния с матрицами

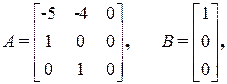
так что k =n =3. Пусть требуется t_р =2с. Тогда из таблицы находим 3 полюса:

-5.0093/2=-2.5047; (-3.9668 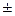j3.7845)/2 = -1.9834 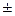j1.8922.

Используем эти полюсы для формирования 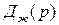и затем определяем векторный коэффициент 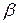обратной связи по состоянию, применяя процедуру acker.

Метод, связанный с многочленами Бесселя, дает неплохие результаты, однако переходная характеристика является слишком медленной, о чем свидетельствует небольшое перерегулирование, получаемое при его использовании.