Размещение полюсов путем введения обратной связи по состоянию (модальное управление).
Метод размещения полюсов, другими словами, модальное управление представляет собой один из фундаментальных методов проектирования систем управления. Его можно рассматривать как обобщение классического метода корневого годографа. Этот метод позволяет построить такую обратную связь по состоянию, при которой все полюсы проектируемой системы принимают заданные значения. При этом предполагается, что все переменные состояния объекта доступны для измерения.
Исходные данные.
1. Будем считать известной математическую модель объекта управления с одним входом и одним выходом
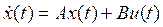 , (1)
, (1)
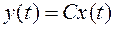 ,
,
где x(t) = [x1(t), x2(t),… xn(t)]’ – n-мерный вектор переменных состояния, u(t) – скалярный управляющий сигнал, y(t) – скалярная управляемая величина, А – постоянная матрица размерности 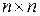 ; В и С – постоянные вектор-столбец и вектор-строка соответственно (в данном случае r=l=1). Предположим, что объект полностью управляемый, а вектор состояния x(t) измерим.
; В и С – постоянные вектор-столбец и вектор-строка соответственно (в данном случае r=l=1). Предположим, что объект полностью управляемый, а вектор состояния x(t) измерим.
2. Предположим, что возмущающее воздействие f(t) представляет собой импульсы, поступающие в случайные моменты ti , i=0,1,2,..(рис. 1).
 Пусть система находится в нулевом состоянии. Тогда каждый из этих импульсов можно трактовать как результата изменения начального состояния объекта. Итак, поступает очередной импульс, вследствие объект переходит из нулевого начального состояния в ненулевое состояние. Затем импульс заканчивается. Отработка возмущающего импульса заключается в возвращении объекта в прежнее нулевое состояние.
Пусть система находится в нулевом состоянии. Тогда каждый из этих импульсов можно трактовать как результата изменения начального состояния объекта. Итак, поступает очередной импульс, вследствие объект переходит из нулевого начального состояния в ненулевое состояние. Затем импульс заканчивается. Отработка возмущающего импульса заключается в возвращении объекта в прежнее нулевое состояние.
3. Критерий качества задается в виде характеристического многочлена желаемой системы
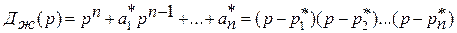 , (2)
, (2)
где 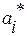 ,
, 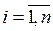 , представляют собой коэффициенты, определяемые заданным расположением полюсов
, представляют собой коэффициенты, определяемые заданным расположением полюсов 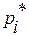 ,
, 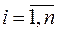 , желаемой системы, другими словами, корней характеристического уравнения
, желаемой системы, другими словами, корней характеристического уравнения 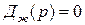 желаемой системы. Итак, свойства желаемой системы определяются расположением ее полюсов.
желаемой системы. Итак, свойства желаемой системы определяются расположением ее полюсов.
Заметим, что в общем случае коэффициенты  характеристического многочлена объекта управления
характеристического многочлена объекта управления 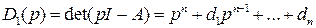 , а, следовательно, и полюсы этого объекта, отличаются от значений
, а, следовательно, и полюсы этого объекта, отличаются от значений 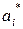 и
и 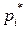 .
.
 4. Цель управления заключается в стабилизации управляемой величины y(t) на нулевом уровне. При этом задающее воздействие принимается равным нулю, v(t)=0. По существу система должна работать так, чтобы привести управляемую величину y(t), следовательно, состояние х(t)в начало координат из начального состояния, обусловленного возмущающим импульсом. В методе размещения полюсов требуемая скорость затухания свободного движения проектируемой системы, то есть длительность процесса перехода системы из ненулевого состояния х(0) в нулевое состояние
4. Цель управления заключается в стабилизации управляемой величины y(t) на нулевом уровне. При этом задающее воздействие принимается равным нулю, v(t)=0. По существу система должна работать так, чтобы привести управляемую величину y(t), следовательно, состояние х(t)в начало координат из начального состояния, обусловленного возмущающим импульсом. В методе размещения полюсов требуемая скорость затухания свободного движения проектируемой системы, то есть длительность процесса перехода системы из ненулевого состояния х(0) в нулевое состояние 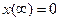 обеспечивается неявно путем фиксации полюсов проектируемой системы. Задача заключается в том, чтобы система была настолько быстродействующей, чтобы могла вернуться в прежнее состояние до прихода следующего импульса. Таким образом, свободное движение системы должно затухать достаточно быстро, а это можно обеспечить за счет правильного (желаемого) размещения полюсов системы. Поэтому рассматриваемая задача называется размещением полюсов системы.
обеспечивается неявно путем фиксации полюсов проектируемой системы. Задача заключается в том, чтобы система была настолько быстродействующей, чтобы могла вернуться в прежнее состояние до прихода следующего импульса. Таким образом, свободное движение системы должно затухать достаточно быстро, а это можно обеспечить за счет правильного (желаемого) размещения полюсов системы. Поэтому рассматриваемая задача называется размещением полюсов системы.
5. Допустимый закон управления c обратной связью по состоянию можно записать в виде
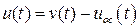 , (3)
, (3)
где скалярная величина 
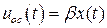 (4)
(4)
называется сигналом обратной связи по состоянию. В уравнение обратной связи по состоянию входит вектор-строка  , называемый векторным коэффициентом обратной связи по состоянию. Учитывая, что вектор состояния
, называемый векторным коэффициентом обратной связи по состоянию. Учитывая, что вектор состояния 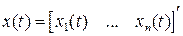 , то есть представляет собой вектор-столбец, сигнал обратной связи
, то есть представляет собой вектор-столбец, сигнал обратной связи 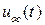 можно рассматривать как скалярное произведение векторов
можно рассматривать как скалярное произведение векторов 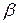 и x(t) и записать в виде линейной комбинации переменных состояния
и x(t) и записать в виде линейной комбинации переменных состояния 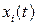 :
:
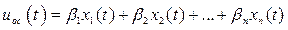 . (5)
. (5)
Элементы 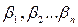 вектора
вектора 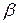 называют скалярными коэффициентами обратной связи по состоянию.
называют скалярными коэффициентами обратной связи по состоянию.
С помощью уравнений (1), (3) и (4) операционную структурную схему проектируемой системы можно представить в виде, показанном на рис. 2.
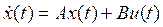 , (1)
, (1)
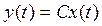 ,
,
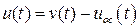 , (3)
, (3)
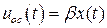 (4)
(4)
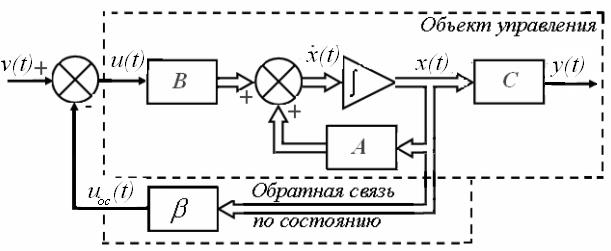
Рис. 2
Заметим, что обратная связь по состоянию является безынерционным (статическим) управляющим устройством (регулятором). Все изменения x(t) приводят к мгновенному изменению 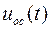 .
.
Подставляя (3) и 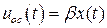 (4) в (1), получаем уравнение состояния проектируемой системы
(4) в (1), получаем уравнение состояния проектируемой системы
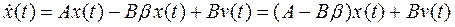 .
.
Запишем его в виде
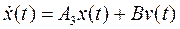 , (6)
, (6)
где
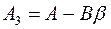 (7)
(7)
является матрицей проектируемой системы (матрицей замкнутой системы).
Используя (7), находим характеристический многочлен проектируемой системы
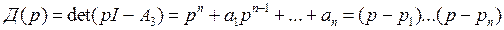 , (8)
, (8)
где 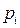 ,
, 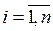 , представляют собой полюсы проектируемой системы. Матрица А3 зависит от выбора
, представляют собой полюсы проектируемой системы. Матрица А3 зависит от выбора 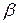 , а следовательно, при изменении вектора
, а следовательно, при изменении вектора 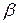 изменяются коэффициенты
изменяются коэффициенты 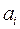 многочлена
многочлена 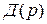 и полюсы
и полюсы 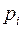 проектируемой системы. Как видим, за счет обратной связи
проектируемой системы. Как видим, за счет обратной связи 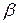 по состоянию оказывается возможным влиять на расположение полюсов проектируемой системы.
по состоянию оказывается возможным влиять на расположение полюсов проектируемой системы.
Дата добавления: 2015-08-14; просмотров: 2101;
