Управляемость и наблюдаемость.
Рассмотрим два фундаментальных свойства систем управления, которые имеют такое же большое значение, как и свойство устойчивости. Первое из них связано с возможностью перевода системы из любого начального состояния в любое другое заданное состояние, а второе – с возможностью определить состояние системы по управляемой величине и управляющему воздействию.
1. Управляемость.
Определение управляемости. Система (управляемая система или объект) с уравнением состояния
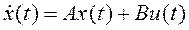 (1)
(1)
является полностью управляемой, если существует управляющий сигнал 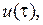
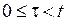 f , который переводит систему из нулевого начального состояния х(0)=0 в момент t0=0в любое другое состояние х(tf)за конечное время tf.
f , который переводит систему из нулевого начального состояния х(0)=0 в момент t0=0в любое другое состояние х(tf)за конечное время tf.
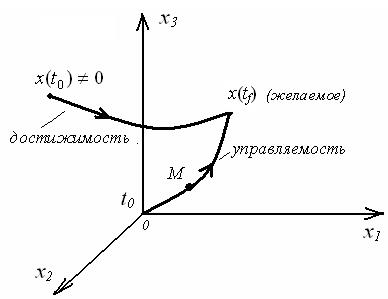 Состояние системы в текущий момент времени t можно изобразить с помощью точки М в пространстве состояния. Под пространством состояния понимаем пространство, осями которого являются переменные состояния.
Состояние системы в текущий момент времени t можно изобразить с помощью точки М в пространстве состояния. Под пространством состояния понимаем пространство, осями которого являются переменные состояния.
Здесь точка М – изображающая точка.
Изменение положения изображающей точки – это переход системы из одного состояния в другое.
Нетрудно показать, что если система полностью управляемая, то ее при некоторых допущениях можно перевести из любого начального состояния в любое другое состояние. Это свойство системы называют достижимостью.
Управляемость – частный случай достижимости.
На рисунке выше дана геометрическая интерпретация свойств управляемости и достижимости.
Теорема Калмана. (О полной управляемости).
Для полной управляемости системы, описываемой уравнением (1), необходимо и достаточно, чтобы матрица управляемости (блочная матрица)
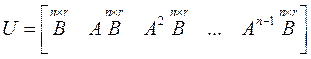 (2)
(2)
имела ранг, равный n, где n – порядок системы: 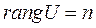 . Матрица U имеет размерность (
. Матрица U имеет размерность ( 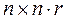 ), так как каждый блок имеет размерность
), так как каждый блок имеет размерность 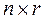 , а всего n блоков (
, а всего n блоков (  столбцов).
столбцов).
Если существует хотя бы один минор n-го порядка 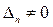 матрицы U , то
матрицы U , то 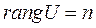 . Минор n-го порядка – определитель матрицы U, составленный из n произвольных столбцов матрицы U.
. Минор n-го порядка – определитель матрицы U, составленный из n произвольных столбцов матрицы U.
Для системы с одним входом, т.е. если 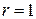 , то U – квадратная матрица
, то U – квадратная матрица 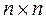 и имеет единственный минор n-го порядка, который совпадает с определителем матрицы
и имеет единственный минор n-го порядка, который совпадает с определителем матрицы 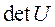 . При этом условие полной управляемости для r=1:
. При этом условие полной управляемости для r=1:
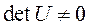 ,
,
то есть матрица управляемости должна быть невырожденной.
Пример. Для двойного интегратора
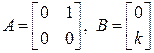 ,
,
где k – коэффициент усиления двойного интегратора.
Является лидвойной интегратор полностью управляемым, и при каких условиях?
В данном случае n=2, 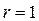 . Следовательно, в соответствии с (2) матрица управляемости двойного интегратора
. Следовательно, в соответствии с (2) матрица управляемости двойного интегратора
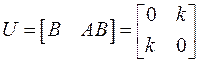 ,
,
так что
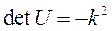 .,
.,
Следовательно, 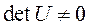 , если
, если 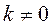 . Это и есть условие полной управляемости двойного интегратора.
. Это и есть условие полной управляемости двойного интегратора.
Команды Matlab: U=ctrb(A,B); r=rank(U).
Замечание 1. Физический смысл свойства полной управляемости заключается в том, что управление 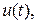 оказывает влияние на каждую из переменных состояния
оказывает влияние на каждую из переменных состояния 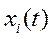 ,
, 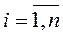 . При этом можно изменять положение изображающей точки произвольно с помощью соответствующего управления.
. При этом можно изменять положение изображающей точки произвольно с помощью соответствующего управления.
Замечание 2. Является ли система полностью управляемой можно определить с помощью операционной структурной схемы. Если на операционной структурной схеме имеются пути, ведущие от управления к каждой переменной состояния, то система является полностью управляемой.
Пример. Рассмотрим операционную структурную схему системы, представленную на рисунке ниже. Здесь 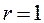 , n=2.
, n=2.
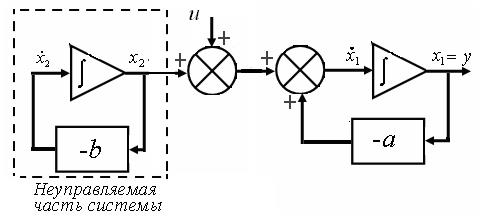
Как видим, управление u будет оказывать влияние лишь на переменную х1. Левая часть структурной схемы ведет себя автономно от управления u. Следовательно, система не является полностью управляемой. Если система не является полностью управляемой, то ее можно разложить на управляемую и неуправляемую части (подсистемы).
Аналитически покажем, что рассматриваемая система не является полностью управляемой. Для этого по структурной схеме найдем уравнения в переменных состояния
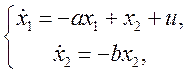
из которых видно, что управление u не влияет на х2 .
Найдем A и B:
 ,
,  .
.
Отсюда матрица управляемости
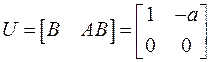 .
.
Как видим, 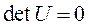 , то есть система не удовлетворяет условию полной управляемости.
, то есть система не удовлетворяет условию полной управляемости.
Замечание 3. Если система с одним входом, другими словами, при r=1, не является полностью управляемой, то ее ПФ вырождается, другими словами, ее ПФ является вырожденной ПФ, то есть порядок знаменателя ПФ будет меньше порядка системы (порядка характеристического уравнения системы).
Отсюда система с одним входом является полностью управляемой, если ее передаточная функция не содержит одинаковых сомножителей в числителе и знаменателе (сокращаемых сомножителей).
Для примера, рассмотренного в замечании 2:
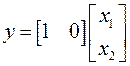 ,
, 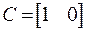 , l=1.
, l=1.
При этом ПФ системы
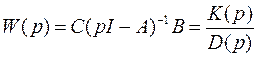 ,
,
где характеристический многочлен
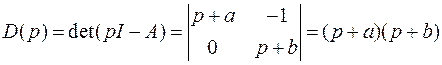 .
.
Следовательно, корни характеристического уравнения 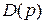 =0, другими словами, полюсы системы равны:
=0, другими словами, полюсы системы равны:  .
.
Найдем числитель 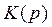 , представляющий собой скалярный многочлен
, представляющий собой скалярный многочлен
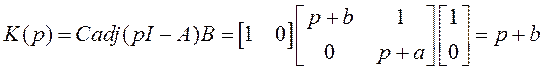 .
.
Итак
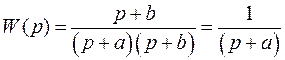 .
.
Порядок системы n=2, а порядок знаменателя ПФ равен 1, то есть передаточная функция системы вырождена. Эта система устойчива по начальным условиям, если 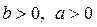 (левые корни). Если
(левые корни). Если 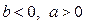 , (
, ( 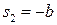 есть правый корень), то система устойчива по входу и неустойчива по начальным условиям. Другими словами, компенсация правых (неминимальнофазовых) нулей системы за счет полюсов последовательно включенной еще одной системы делает последовательное соединение не стабилизируемым.
есть правый корень), то система устойчива по входу и неустойчива по начальным условиям. Другими словами, компенсация правых (неминимальнофазовых) нулей системы за счет полюсов последовательно включенной еще одной системы делает последовательное соединение не стабилизируемым.
Модель в виде ПФ может быть только частичным описанием системы.
Замечание 4. Система, описываемая уравнением (1), называется стабилизируемой, если неуправляемая часть является устойчивой по начальным условиям. Для рассмотренного в замечании 2 примера условие стабилизируемости системы: 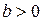 .
.
Свойство стабилизируемости позволяет за счет обратной связи обеспечить устойчивость замкнутой системы даже тогда, когда объект управления содержит неуправляемую часть. Включение неуправляемой части в модель системы достаточно общий случай. Это удобно для описания различных возмущающих воздействий. Например, постоянное возмущающее воздействие можно задать в пространстве состояний как 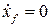 .
.
Замечание 5. Ранг матрицы управляемости не зависит от выбора вектора состояния. Другими словами, ранг матрицы управляемости является инвариантом, т.е.
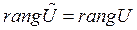 ,
,
где
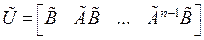 =TU
=TU
представляет собой матрицу управляемости преобразованной системы, описываемой
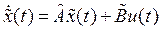 .
.
Дата добавления: 2015-08-14; просмотров: 12487;
