Установившаяся реакция многомерной системы.
Рассмотрим систему, описываемую в переменных состояния
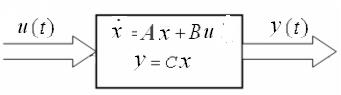
Мы показали, что
y 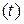 =yсв
=yсв 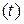 +yвын
+yвын 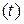 .
.
Если система устойчивая по начальным условиям, то
y 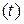 =yпер
=yпер 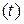 +yуст
+yуст 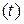 ,
,
причем переходной процесс yпер 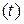 затухает, т. е.
затухает, т. е.
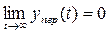 ,
,
а установившийся процесс описывается выражением
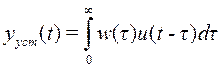 , (*)
, (*)
где 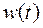 - матричная весовая функция.
- матричная весовая функция.
Рассмотрим два случая:
1. Пусть входной сигнал u(t) – векторный гармонический сигнал, записанный в показательной форме
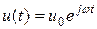 , (1)
, (1)
где постоянный вектор 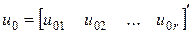 - векторная амплитуда гармонического сигнала,
- векторная амплитуда гармонического сигнала, 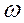 - частота гармонического сигнала.
- частота гармонического сигнала.
Найдем установившуюся реакцию: yуст 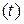 - ?.
- ?.
Подставим (1) в (*), получаем
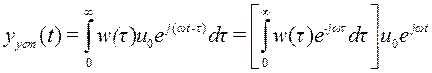 ,
,
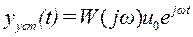 , (2)
, (2)
где матрица ( 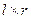 )
)
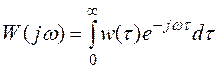
- матричная АФХ многомерной системы.
Так как матричная ПФ определяется как
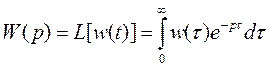 ,
,
то
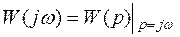 .
.
Заметим, что мы не можем построить годограф 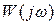 для многомерной системы в отличие от одномерной, потому что
для многомерной системы в отличие от одномерной, потому что 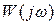 - матрица.
- матрица.
Введем понятие скалярных АФХ. Запишем матричную АФХ в символической форме 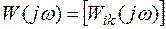 , где
, где 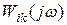 - (i, k)-ый элемент
- (i, k)-ый элемент 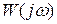 . Напомним, что матричная ПФ
. Напомним, что матричная ПФ
 ,
, 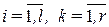 ,
,
где 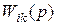 - скалярная ПФ, связывающая преобразование Лапласа i –го выхода с преобразованием k –го входа, так что,
- скалярная ПФ, связывающая преобразование Лапласа i –го выхода с преобразованием k –го входа, так что,  если
если 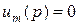 ,
, 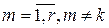 ,то
,то
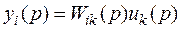 .
.
Следовательно, скалярная АФХ связана со скалярной ПФ как
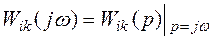 .
.
Отсюда можно выяснить физический смысл скалярной АФХ: 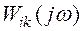 определяет установившуюся реакцию, получаемую на i-том выходе при подаче на k -й вход гармонического сигнала, при этом сигналы на остальных входах отсутствуют и система предварительно невозбуждена, т. е.
определяет установившуюся реакцию, получаемую на i-том выходе при подаче на k -й вход гармонического сигнала, при этом сигналы на остальных входах отсутствуют и система предварительно невозбуждена, т. е.
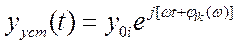 ,
,
где
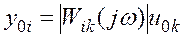 - амплитуда установившейся реакции на i-ом выходе,
- амплитуда установившейся реакции на i-ом выходе,

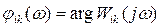 - фаза установившейся реакции на i-ом выходе.
- фаза установившейся реакции на i-ом выходе.
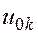 - амплитуда гармонического сигнала на k-ом входе.
- амплитуда гармонического сигнала на k-ом входе.
2. Пусть входной сигнал u(t) - постоянный вектор
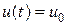 .
.
Найдем yуст(t), используя 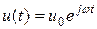 (1) и
(1) и 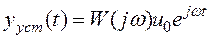 (2). Так как постоянный вектор можно рассматривать как частный случай гармонического сигнала при
(2). Так как постоянный вектор можно рассматривать как частный случай гармонического сигнала при 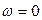 , то установившаяся реакция
, то установившаяся реакция
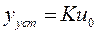
представляет собой постоянный вектор. Здесь
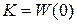
- матричный коэффициент усиления многомерной системы.
В символическом виде:
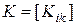 ,
,
где
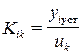 - скалярный коэффициент усиления.
- скалярный коэффициент усиления.
Ранее показали, что ПФ определяется как 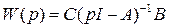 . Следовательно, матричный коэффициент усиления
. Следовательно, матричный коэффициент усиления
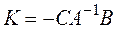
определяется посредством А, В, С.
Преобразование переменных состояния. Инварианты.
Уравнения движения линейной системы:
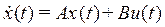 ,
, 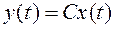 , (1)
, (1)
путем введения другого вектора состояния
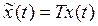 , (2)
, (2)
связанного с исходным вектором состояния x(t) с помощью невырожденной матрицы (матрицы подобия) Т размерности  , можно преобразовать к виду
, можно преобразовать к виду
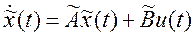 ,
, 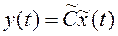 , (3)
, (3)
где
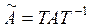 ,
, 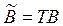 ,
, 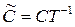 . (4)
. (4)
Переход от (1) к (3) называется преобразованием подобия.
Так как матрица Т невырожденная, то 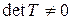 и обратная матрица
и обратная матрица 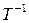 существует, так что
существует, так что 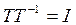 . Уравнения (3) описывают ту же систему, что и исходные уравнения, т. е. преобразованные уравнения эквивалентны исходным. Эквивалентность здесь понимается следующим образом. Если на вход систем, описываемых уравнениями (1) и (3), подать один и тот же сигнал
. Уравнения (3) описывают ту же систему, что и исходные уравнения, т. е. преобразованные уравнения эквивалентны исходным. Эквивалентность здесь понимается следующим образом. Если на вход систем, описываемых уравнениями (1) и (3), подать один и тот же сигнал 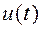 , а начальное состояние второй системы связать с начальным состоянием первой системы соотношением
, а начальное состояние второй системы связать с начальным состоянием первой системы соотношением 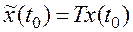 , то на выходе обеих систем получим одинаковый сигнал
, то на выходе обеих систем получим одинаковый сигнал 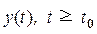 . Таким образом, выбор вектора состояния
. Таким образом, выбор вектора состояния  неоднозначен и вид матриц А, В, С зависят от этого выбора.
неоднозначен и вид матриц А, В, С зависят от этого выбора.
Инварианты. Определенный интерес представляют инварианты – величины и функции, которые не зависят от выбранного вектора состояния, т. е. не зависят от выбора матрицы преобразования Т. К числу инвариантов, в частности, относятся передаточная функция и характеристический многочлен системы.
a. Передаточная функция преобразованной системы 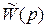 равна передаточной функции исходной системы
равна передаточной функции исходной системы
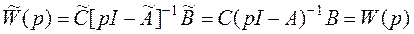 ,
,
что и нетрудно доказать.
b. Характеристический многочлен преобразованной системы 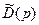 равен характеристическому многочлену исходной системы
равен характеристическому многочлену исходной системы 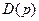 , так что
, так что
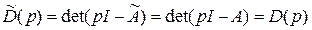 .
.
Итак, характеристический многочлен инвариантен к выбору вектора состояния  . Следовательно, собственные числа
. Следовательно, собственные числа 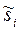 матрицы
матрицы 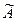 равны собственным числам
равны собственным числам 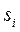 матрицы А, т. е.
матрицы А, т. е. 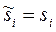 ,
,  .
.
Отсюда собственные числа, другими словами корни характеристического уравнения системы, инвариантны к выбору вектора состояния. Таким образом, путем подбора матрицы Т нельзя неустойчивую систему превратить в устойчивую, т. е. устойчивость линейной системы не зависит от принятой формы математической модели, а является ее внутренним свойством.
Дата добавления: 2015-08-14; просмотров: 1154;
