Лекция 4. Цель введения новых переменных состояния – получение более простой формы матриц А, В, С, а следовательно и уравнений системы.

Цель введения новых переменных состояния 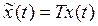– получение более простой формы матриц А, В, С, а следовательно и уравнений системы.

Из различных канонических форм в данном курсе будут использоваться управляемая каноническая форма, которую называют также просто управляемой формой, и наблюдаемая каноническая форма.

Пусть система с одним входом и одним выходом описывается уравнениями (1) 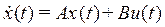, 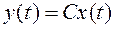. Тогда путем соответствующего выбора матрицы Т эти уравнения можно привести к управляемой канонической форме, имеющей вид уравнений (3) 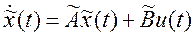, 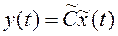при

, .

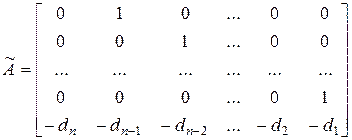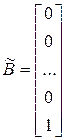Здесь 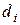, , 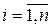являются коэффициентами характеристического многочлена системы

.

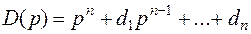Преимущество управляемой формы заключается в простоте вычислений передаточной функции и закона управления с обратной связью по состоянию (см. ниже).

Для систем с одним входом и одним выходом к каноническим формам уравнений в переменных состояния можно придти другим путем, не прибегая к помощи матрицы T, а именно используя передаточную функцию системы. Передаточная функция системы с одним входом и одним выходом имеет вид

.

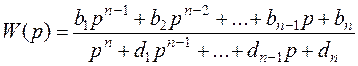При этом уравнения в переменных состояния, как показано, могут быть представлены в следующих канонических формах:

1. Управляемая каноническая форма:

, .

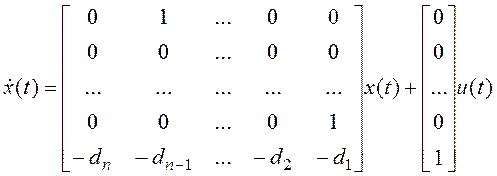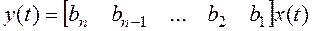2. Наблюдаемая каноническая форма:

, .

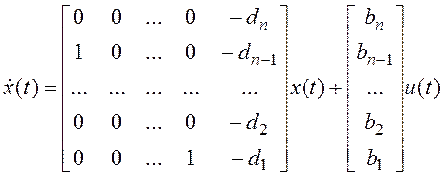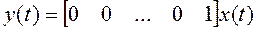Такое преобразование применимо к ПФ, описывающей минимальную реализацию (представление) математической модели системы, которую (реализацию) можно найти путем сокращения всех одинаковых сомножителей в числителе и знаменателе исходной ПФ. Уравнения в переменных состояния, соответствующие ПФ 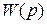системы, называют реализацией системы.

Минимальная реализация определяется как математическая модель самого низкого порядка из множества моделей, обеспечивающих то же самое преобразование «вход-выход». Возможность перехода к каноническим формам уравнений в переменных состояния тесно связана со свойствами управляемости и наблюдаемости системы.