Лекция 3. Для линейных стационарных систем преобразование вход-выход определяется с помощью ПФ W(p)

Для линейных стационарных систем преобразование вход-выход определяется с помощью ПФ W(p). При этом L₂ - индуцированная норма (*) равна - норме (бесконечной норме или эйч бесконечной норме) передаточной функции, определяемой как

.

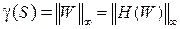Для одномерных систем эта норма равна максимальному значению АЧХ системы,

,

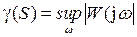если W(p) не имеет правых полюсов.

Пример 1. 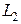- коэффициент усиления линейной статической системы (усилительного звена). Выходной сигнал y такой системы связан с входным сигналом u посредством уравнения

,

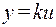где k есть коэффициент усиления в обычном понимании этого названия.

Тогда квадрат второй нормы выходного сигнала такого линейной системы

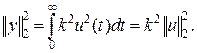
Отсюда 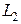- коэффициент усиления линейной статической системы

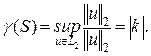
Пример 2. 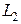- коэффициент усиления устойчивой одномерной линейной системы. Предположим, что АЧХ линейной одномерной системы 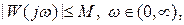и 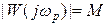для некоторого 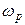. Тогда на основании теоремы Парсеваля квадрат второй нормы выходного сигнала линейной одномерной системы

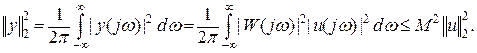
Равенство имеет место при .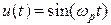

Следовательно, 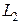- коэффициент усиления устойчивой одномерной линейной системы

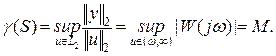
Пусть ПФ системы

,

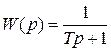где T положительная постоянная. Просто находим L₂ - индуцированную норму

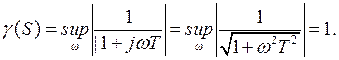
Для многомерной линейной системы L₂ - индуцированная норма равна

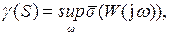
где 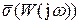самое большое сингулярное число W(p).

Дадим понятие сингулярных чисел применительно к матрице A. Собственные значения 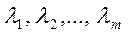матрицы 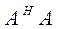будут вещественными (наибольшее 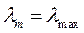и наименьшее 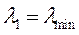собственные значения). Здесь 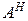является эрмитовой матрицей, т.е. транспонированной комплексно- сопряженной матрицей 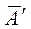. Самое большое (максимальное) сингулярное число матрицы A определяется как

.

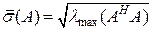При этом имеет место неравенство

.

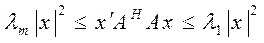Пример.

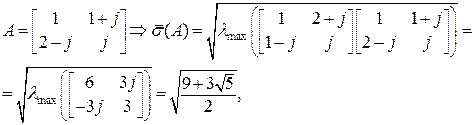
т.к. характеристическое уравнение

матрицы 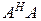имеет вещественные корни

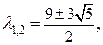
являющиеся собственными значениями этой матрицы.

Определение: Сингулярными значениями матрицы 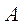называют величины , где 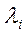являются собственными значениями матрицы .

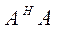Наибольшее сингулярное значение обозначается как .

Наименьшее сингулярное значение обозначается как .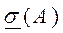

Показано, что L₂ - коэффициент усиления матрицы 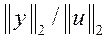находится между наименьшим и наибольшим сингулярными значениями:

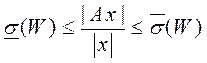. (1)

Функция MATLAB sigma (W) вычисляет все сингулярные числа системы.

Пример. Пусть ПФ системы

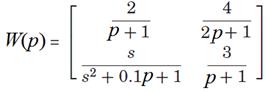
Используя sigma (W), находим графики зависимости и .

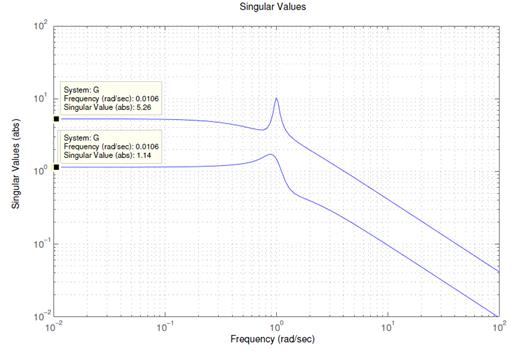
Используя команду norm (W,inf) вычисляем .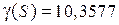

Определение. Система S называется устойчивой с точки зрения «ограниченный вход – ограниченный выход» (ОВОВ устойчивой) или, другими словами, L₂ - устойчивой, если ее L₂ - коэффициент усиления является (ограниченным) конечным,

< .

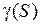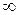Теорема о малом коэффициенте усиления.

Многие системы управления с обратной связью могут быть представлены структурно в виде, показанном на рис. ниже. Здесь v₁ и v₂ внешние воздействия, оказывающие влияние посредством опрераторов S₁ и S₂ на сигналы e₁ и e₂ .

Пусть S₁ и S₂ представлют собой ОВОВ устойчивые системы .

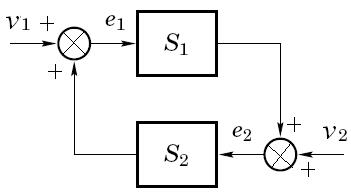
Если

,

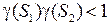то замкнутая система при входах (v₁, v₂) и выходах (e₁,e₂) является ОВОВ устойчивой, т.е. 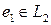и .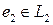

Док-во. Докажем теорему для каждого сигнала e₁ и e₂ . Используя второе свойство нормы и неравенство 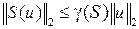, которое вытекает из определения коэффициента усиления 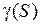системы, получаем

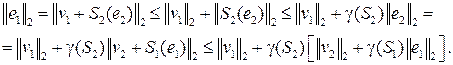
Отсюда

Если 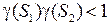, 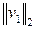< 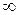, 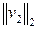< 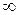, то < .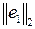

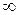Аналогично получаем

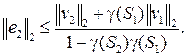
что нас приводит к выводу, что < .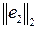

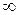Замечание 1. Знаки суммирования сигналов не играют роли, т.к.

.

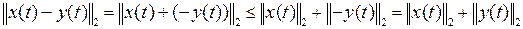Замечание 2. Теорема не предполагает линейности или стационарности и поэтому справедлива не только для линейных стационарных систем, но и для линейных нестационарных систем, и для нелинейных систем.

Примером рассматриваемой системы может служить система с обратной связью, для которой в качестве оператора 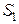фигурирует ПФ управляющего устройства 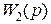, в качестве оператора 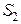- ПФ ОУ 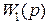, в качестве сигналов 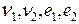- соответственно задающее воздействие 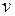, возмущающее воздействие 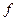, ошибка управления 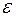и управляющее воздействие 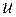. Если ОУ с одним входом и одним выходом является устойчивым и для него L₂ - коэффициент усиления 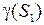= M, а в качестве управляющего устройства используется пропорциональный регулятор с L₂ - коэффициентом усиления 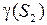=|k|, то замкнутая система будет ОВОВ устойчивой при условии, что |k| M<1.